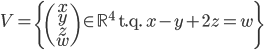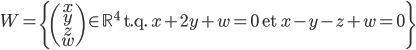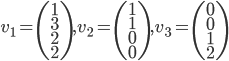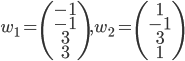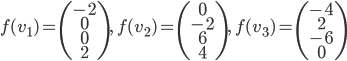Self-Avoiding Walks on Random Quadrangulations
The local limit of random quadrangulations (UIPQ) and the local limit of quadrangulations with a simple boundary (the simple boundary UIHPQ) are two very well studied objects. We shall see how the simple boundary UIHPQ relates to an annealed model of self-avoiding walk on random quadrangulations, and how metric information obtained for the UIHPQ can be used to study quantities such as the displacement of the self-avoiding walk from the origin, as well as to ultimately investigate how the biasing of random quadrangulations by the number of their self-avoiding walks affects their local limit.
Croisements inéluctables et preuves au hasard
 If you're ever in Lyon on a Wednesday, make sure not to miss the Séminaire de la détente at the MMI! Cake, tidbits of mathematical fun, plus even a great apéro afterwords: what's there not to love?!
If you're ever in Lyon on a Wednesday, make sure not to miss the Séminaire de la détente at the MMI! Cake, tidbits of mathematical fun, plus even a great apéro afterwords: what's there not to love?!
Was so happy to give a talk there in September: thanks to Olga and Marie for the invitation and delicious cake! Here's the abstract and slides (as usual, a version in a better format, possibly with some added explanations – some essential bits were done on the blackboard – may or may not be on the way):
For an English version of the following abstract, click here.
Nous sommes en 1944 ; le mathématicien Pál Turán, qui se trouve dans un camp de travail près de Budapest, est chargé de transporter des briques des fours aux aires de stockage via des chariots sur rails. Chaque four est relié par des rails à chacune des aires de stockage ; pousser les chariots ne demande pas trop d’effort, sauf aux croisements de deux rails, où ils ont tendance à capoter, de sorte que la plupart des briques tombent dehors. Pourquoi – s’interroge Pál – construire ce réseau de manière aussi inefficace, avec tellement de croisements exaspérants ?! Comment pourrait-on minimiser le nombre de croisements, tout en reliant chaque four à chaque aire de stockage ?
C’est peut-être la première question (qui est encore essentiellement ouverte !) portant sur le ’nombre de croisements’, une notion importante en théorie des graphes. En l’étudiant, on va ’croiser’ des artistes constructivistes, des informaticiens, des matheux sceptiques, et on va finalement tomber sur l’une des parties les plus précieuses de l’héritage de Pál Erdős : la méthode que l’on appelle ’probabiliste’.
Corrigé exo 3 feuille 5 (?)
Une entreprise fabrique des pièces d’usines. Parmi les pièces fabriquées, 90 % satisfont aux normes de qualité, 5 % ne satisont pas à ces normes mais fonctionnent quand même et 5 % sont défectueuses. Pour essayer de connaître la fiabilité du fabricant, un client potentiel choisit au hasard 2 pièces. On appelle
le nombre de pièces défectueuses et
le nombre de pièces aux normes.
1. Calculer la loi du coupleet sa matrice de variance-covariance.
2. Trouver les lois deet de
, puis leurs espérances.
3. Retrouver ce dernier résultat en utilisant le principe de linéarité de l’espérance.
4.et
sont-elles indépendantes ?
Il est important de bien comprendre la situation decrite dans l'exo : les pièces fabriquées tombent chacune dans une de trois catégories :
- pièces aux normes (
 )
) - pièces fonctionnantes, mais pas aux normes (
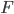 )
) - pièces défectueuses (bien sûr, pas aux normes) (
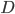 )
)
Les trois ensambles 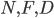 forment une partition de l'ensamble de pièces, au sens où il n'y a pas d'intersection entre chaque couple d'ensembles (il ne peut pas y avoir, par exemple, une pièce defectueuse mais aux normes, ou une pièce qui est dans
forment une partition de l'ensamble de pièces, au sens où il n'y a pas d'intersection entre chaque couple d'ensembles (il ne peut pas y avoir, par exemple, une pièce defectueuse mais aux normes, ou une pièce qui est dans 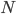 et
et 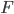 en même temps).
en même temps).
On prend deux pièces au hazard ; on va les appeler 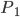 et
et 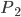 . Pour chaque pièce (de manière indépendante) on a
. Pour chaque pièce (de manière indépendante) on a 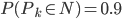 et
et 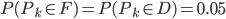 . On se demande combien de pièces sont défectueuses (
. On se demande combien de pièces sont défectueuses ( ) et combien sont aux normes (
) et combien sont aux normes ( ) parmi les deux pièces choisies, et on cherche à déterminer la loi du couple
) parmi les deux pièces choisies, et on cherche à déterminer la loi du couple 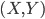 .
.
Les valeurs possibles pour  sont
sont 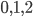 : soit les deux pièces sont défectueuse, soit il y a une qui est défectueuse et une qui marche, soit les deux pièces sont fonctionnantes. De même, les valeurs possibles pour
: soit les deux pièces sont défectueuse, soit il y a une qui est défectueuse et une qui marche, soit les deux pièces sont fonctionnantes. De même, les valeurs possibles pour  sont
sont 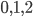 .
.
Il faut donc calculer 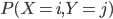 pour
pour 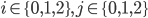 (c'est à dire qu'il y a 9 valeurs à calculer) ; on va considérer chaque cas :
(c'est à dire qu'il y a 9 valeurs à calculer) ; on va considérer chaque cas :
- il est immédiat de voir que
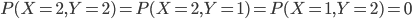 , car ces situations sont impossibles : on n'a que deux pièce, et on sait que si une pièce est défectueuse alors elle n'est pas aux normes et inversement ;
, car ces situations sont impossibles : on n'a que deux pièce, et on sait que si une pièce est défectueuse alors elle n'est pas aux normes et inversement ; 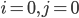 : cela correspond à
: cela correspond à 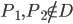 et
et 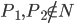 , donc
, donc 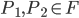 ; comme
; comme 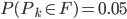 ,
, 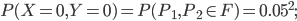
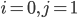 : on a une pièce aux normes ; comme aucune pièce n'est défectueuse, l'autre pièce doit être dans
: on a une pièce aux normes ; comme aucune pièce n'est défectueuse, l'autre pièce doit être dans 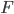 (elle n'est pas défectueuse ni aux normes) ; on a donc
(elle n'est pas défectueuse ni aux normes) ; on a donc 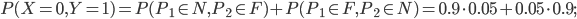
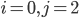 : les deux pièce sont aux normes, ce qui arrive avec proba
: les deux pièce sont aux normes, ce qui arrive avec proba 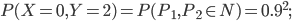
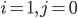 : une pièce défectueuse, l'autre pas aux normes (mais fonctionnante) ;
: une pièce défectueuse, l'autre pas aux normes (mais fonctionnante) ; 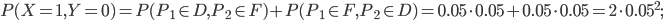
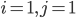 : une pièce défectueuse, l'autre aux normes ;
: une pièce défectueuse, l'autre aux normes ; 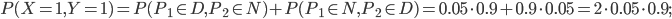
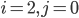 : les deux pièces sont défectueuses ;
: les deux pièces sont défectueuses ; 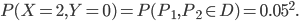
On trouve donc le tableau suivant pour la loi du couple :
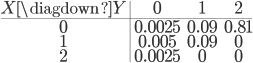
dont les lois marginales et espérances
\begin{array}{c|ccc|c} X & 0 & 1 & 2 & E(X) \\\hline & 0.9025 & 0.095 & 0.0025 & 0.1\end{array}\begin{array}{c|ccc|c} Y & 0 & 1 & 2 & E(Y) \\\hline & 0.01 & 0.18 & 0.81 & 1.8\end{array}
On nous demande aussi de retrouver les espérances en utilisant la linéarité ; ça serait plus simple à faire si on savait ce que c'est que 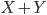 , mais tout ce qu'on sait est que
, mais tout ce qu'on sait est que 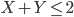 . Par ailleurs, si on appelle
. Par ailleurs, si on appelle 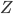 le nombre de pièces fonctionnantes mais pas aux normes parmi les deux, on sait que
le nombre de pièces fonctionnantes mais pas aux normes parmi les deux, on sait que 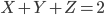 (le nombre totale de pièces) et on sait aussi que, comme la proba qu'une pièce soit dans
(le nombre totale de pièces) et on sait aussi que, comme la proba qu'une pièce soit dans  est la même que celle d'être dans
est la même que celle d'être dans  , la loi de
, la loi de  est la même que la loi de
est la même que la loi de  . On a alors
. On a alors 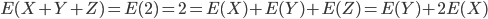 , d'où
, d'où 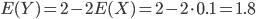 , ce qui est bien ce qu'on avait trouvé avec le calcul direct de
, ce qui est bien ce qu'on avait trouvé avec le calcul direct de 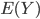 .
.
Finalement,  et
et  ne sont pas indépendants ; cela est bien évident (par exemple, si
ne sont pas indépendants ; cela est bien évident (par exemple, si 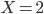 alors il est impossible d'avoir
alors il est impossible d'avoir 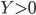 : plus
: plus  est grand, plus
est grand, plus  doit être petit), mais on va calculer la matrice variance-covarance, comme on nous demande de faire dans la première question. On a :
doit être petit), mais on va calculer la matrice variance-covarance, comme on nous demande de faire dans la première question. On a :
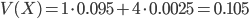
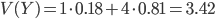
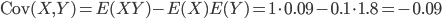
La covariance est non nulle, donc  et
et  ne sont pas indépendants. La matrice variance-covariance est la suivante :
ne sont pas indépendants. La matrice variance-covariance est la suivante :
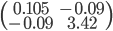
Math207 – Corrigé de l'exo 11 (feuille 3)
Lors de la fête de l'école de Madame Dubois, une tombola est organisée. Il y a deux boîtes de tickets de tombola, une jaune et une rose. Dans la boîte jaune, il y a un ticket gagnant sur trois tandis que dans la boîte rose, il y en a deux sur trois.
1) Un enfant se rend au stand de la tombola et donne son ticket, quelle est la probabilité qu'il gagne un lot? Définir deux espaces de probabilités
et
correspondant aux contenus des deux boîtes.
Comme d'habitude, il y a plusieurs manières possibles de définir des espaces de probabilité pour l'expérience donnée ; voici deux réponses sur lesquelles réfléchir.
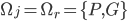 : en tout cas, les résultats possibles de l'expérience aléatoire sont deux ; soit l'enfant a un ticket perdant soit un ticket gagnant. Ce qui change pour les deux boîtes est la proba que le ticket soit gagnant: on a
: en tout cas, les résultats possibles de l'expérience aléatoire sont deux ; soit l'enfant a un ticket perdant soit un ticket gagnant. Ce qui change pour les deux boîtes est la proba que le ticket soit gagnant: on a 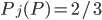 et
et 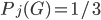 , alors que
, alors que 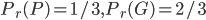 . Ces deux espaces sont parfaitement adaptés à l'expérience "un enfant donne sont ticket, pioché au hasard de la boite jaune/rose", mais on pourrait bien imaginer des univers qui gardent plus d'information sur ce qui est en train de se passer, et qui pourraient être utiles si, dans la même situation (boîte jaune/rose avec un certain nombre de tickets gagnants/perdants), on s'intéressait à une expérience plus complexe (e.g. deux enfants piochent et rendent leur tickets). Par exemple :
. Ces deux espaces sont parfaitement adaptés à l'expérience "un enfant donne sont ticket, pioché au hasard de la boite jaune/rose", mais on pourrait bien imaginer des univers qui gardent plus d'information sur ce qui est en train de se passer, et qui pourraient être utiles si, dans la même situation (boîte jaune/rose avec un certain nombre de tickets gagnants/perdants), on s'intéressait à une expérience plus complexe (e.g. deux enfants piochent et rendent leur tickets). Par exemple :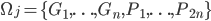 ,
, 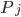 uniforme;
uniforme; 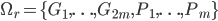 ,
, 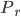 uniforme. Ces espaces gardent l'information de l'"identité" du ticket spécifique pioché par l'enfant (autrement dit, on suppose que les ticket dans chaque boîte soient distinguables, et qu'il y ait
uniforme. Ces espaces gardent l'information de l'"identité" du ticket spécifique pioché par l'enfant (autrement dit, on suppose que les ticket dans chaque boîte soient distinguables, et qu'il y ait 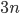 ticket dans la boîte jaune – dont
ticket dans la boîte jaune – dont 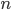 gagnants – et
gagnants – et 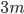 dans la rose – dont
dans la rose – dont  gagnants). Pour chaque boîte, la proba à mettre sur l'ensemble des tickets (si l'on suppose qu'un enfant en pioche un au hasard) est uniforme. Si on allait calculer la proba pour l'enfant de gagner avec ces espaces, on devrait calculer
gagnants). Pour chaque boîte, la proba à mettre sur l'ensemble des tickets (si l'on suppose qu'un enfant en pioche un au hasard) est uniforme. Si on allait calculer la proba pour l'enfant de gagner avec ces espaces, on devrait calculer 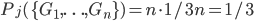 (boîte jaune) et
(boîte jaune) et 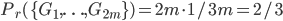 (boîte rose). En fait on n'utilisera pas ces espaces, même si l'on pourrait les adapter au cas de
(boîte rose). En fait on n'utilisera pas ces espaces, même si l'on pourrait les adapter au cas de 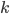 enfants qui piochent leur tickets, parce qu'on ne connait pas les nombres
enfants qui piochent leur tickets, parce qu'on ne connait pas les nombres 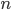 ,
, 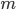 de tickets dans les deux boîtes : on nous dit seulement que ces nombres sont très grands, ce qui veut dire que la proba de piocher un ticket gagnant ne change (presque) pas même si un certain (petit) nombre de tickets a déjà été pioché de la boîte.
de tickets dans les deux boîtes : on nous dit seulement que ces nombres sont très grands, ce qui veut dire que la proba de piocher un ticket gagnant ne change (presque) pas même si un certain (petit) nombre de tickets a déjà été pioché de la boîte.
Le nombre de tickets contenus dans les deux boîtes est très grand et on peut supposer que les proportions de tickets gagnants ne changent pas si on enlève vingt-sept tickets de l'une ou l'autre des boîtes. Bien entendu, les enseignants ne sont pas au courant de la répartiton faite par la directrice. Madame Dubois a choisi une des deux boîtes au hasard dans le bureau de la directrice, elle revient dans sa classe et distribue un ticket aux vingt-sept enfants de sa classe.
Le fils de la directrice est au courant de la répartition des boîtes et tient le stand de la tombola, c'est au tour des élèves de la classe de Madame Dubois de venir voir s'ils ont gagné.2a) Le fils de la directrice compte le nombre de perdants avant qu'il y ait un premier gagnant. Modéliser cette expérience, on notera
la variable aléatoire, calculer sa loi. (On fera attention à bien distinguer les boîtes
jaune et rose.)
Comment modeliser cette expérience aléatoire ? Quels sont les différents résultats que le fils de la directrice pourrait voir ? Il va noter le résultat de chacun des 27 élèves de la classe (gagnant/perdant), dans l'ordre dans lequel ils rendent leurs tickets. Un univers valable est donc 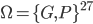 (chaque élément d'
(chaque élément d'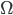 est une séquence de 27 lettres, chacune égale à
est une séquence de 27 lettres, chacune égale à 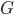 ou
ou 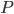 ). Si la boîte est la jaune, chaque enfant a une probe de 1/3 de gagner, et donc, étant donné
). Si la boîte est la jaune, chaque enfant a une probe de 1/3 de gagner, et donc, étant donné 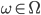 , on a
, on a 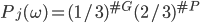 ; si la boîte est la rose, on a
; si la boîte est la rose, on a 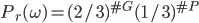 . Sur cet espace, on veut définir une variable aléatoire
. Sur cet espace, on veut définir une variable aléatoire  qui compte le nombre de perdants avant d'avoir un gagnant ;
qui compte le nombre de perdants avant d'avoir un gagnant ; 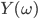 est donc le nombre de
est donc le nombre de 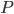 initiales d'
initiales d'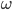 (avant d'avoir un
(avant d'avoir un 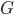 ), par exemple :
), par exemple :
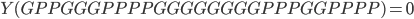
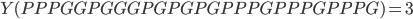
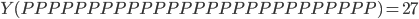
L'ensemble des valeurs possibles de  est donc
est donc 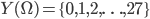 , et si
, et si 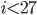 on a
on a 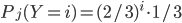 et
et 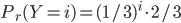 (proba d'avoir
(proba d'avoir 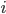 Ps, puis un G avec la boîte jaune/rose). Comme il n'y a que 27 élèves, on a
Ps, puis un G avec la boîte jaune/rose). Comme il n'y a que 27 élèves, on a 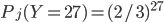 et
et 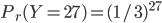 (proba de l'unique séquence avec 27 Ps). La loi de
(proba de l'unique séquence avec 27 Ps). La loi de  est donc très proche d'une loi géométrique de paramètre
est donc très proche d'une loi géométrique de paramètre 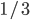 ou
ou 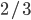 , sauf que, comme
, sauf que, comme 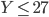 , il faut calculer
, il faut calculer 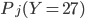 et
et 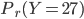 comme l'on a fait, et on a
comme l'on a fait, et on a 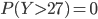 (ce qui n'est pas le cas pour la loi géométrique, qui peut prendre des valeurs arbitrairement grandes !).
(ce qui n'est pas le cas pour la loi géométrique, qui peut prendre des valeurs arbitrairement grandes !).
2b) Calculer la probabilité
et
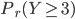
On a
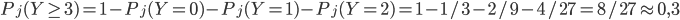
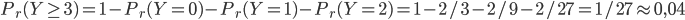
2c) Le premier gagnant de la loterie est le cinquième joueur. Que pouvez-vous supposer ?
On va calculer la probabilité que le premier gagnant soit le cinquième enfant dans le cas de la boîte jaune
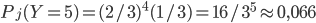
et de la boîte rose
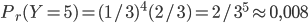 .
.
On voit que la proba de 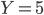 quand la boîte est rose est extrêmement petite, et que la proba du même événement dans le cas de la boîte jaune est 8 fois plus grande. Par conséquence, on peut supposer que la boîte choisie par Madame Dubois soit la jaune.
quand la boîte est rose est extrêmement petite, et que la proba du même événement dans le cas de la boîte jaune est 8 fois plus grande. Par conséquence, on peut supposer que la boîte choisie par Madame Dubois soit la jaune.
Le fils de la directrice est quasiment sûr que Madame Dubois a choisi la boîte jaune, on va donc travailler avec cette hypothèse dans cette question.
3a) Les vingt-sept enfants de la classe de Madame Dubois ont donné leur ticket de tombola, quelle est la loi du nombre de gagnants ? On notera
cette variable aléatoire et on calculera sa loi, son espérance et sa variance. (Bien justifier le calcul de la loi.)
On va utiliser l'espace probabilisé décrit lors de la question précédente, et on va définir 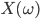 comme le nombre de
comme le nombre de 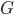 qui apparaissent dans la séquence
qui apparaissent dans la séquence 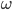 ; on pose
; on pose 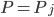 . On a donc
. On a donc
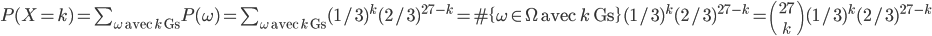
La variable  suit donc une loi binomiale de paramètres
suit donc une loi binomiale de paramètres  et
et 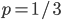 ; son espérance est
; son espérance est 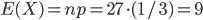 et sa variance est
et sa variance est 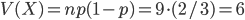 .
.
3b) À l'aide de l'inégalité de Bienaymé-Tchebichev majorer
.
3c) En déduire une minoration de la probabilité que le nombre de gagnants de la classe de Madame Dubois soit compris entre 7 et 11.
3d) Il y a 12 élèves qui ont un ticket gagnant, que pouvez-vous en conclure ?
Par Bienaymé-Tchebichev
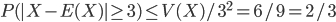 .
.
On a donc 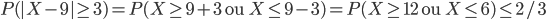 .
.
En passant au complémentaire
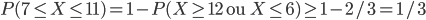 .
.
Le fait qu'il y ait exactement 12 tickets gagnants dans la classe est bien compatible avec ces estimations : on n'a pas une majoration assez forte de 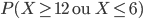 pour dire que le résultat est incompatible avec le fait que la boîte soit la jaune (et en fait même si
pour dire que le résultat est incompatible avec le fait que la boîte soit la jaune (et en fait même si 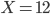 serait un peu surprenant, les calculs faits ne nous permettent pas de mettre en doute l'hypothèse du fils de la directrice).
serait un peu surprenant, les calculs faits ne nous permettent pas de mettre en doute l'hypothèse du fils de la directrice).
Math207 – Corrigé de l'exo 6 (feuille 3)
Soit
une variable aléatoire de loi uniforme sur
. Soit
une variable al\'eatoire de loi uniforme sur
. Donner un sens mathématique à la phrase précédente ; donner la loi de
, et calculer l'espérance de
en fonction de
.
On sait que, quand 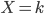 , "la variable
, "la variable  est uniforme sur
est uniforme sur  ", ce qui veut dire que pour
", ce qui veut dire que pour 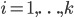 , on a
, on a 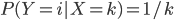 .
.
Les valeurs possibles de  sont
sont 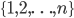 , et pour calculer
, et pour calculer 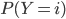 (
(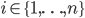 ) il faut d'abord distinguer les cas possibles pour la valeur de
) il faut d'abord distinguer les cas possibles pour la valeur de  . On a
. On a
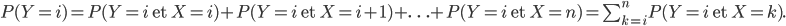
Mais 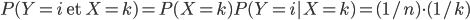 (si
(si 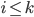 ) et donc
) et donc
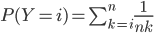 .
.
On a alors 
Soit
une variable aléatoire de loi uniforme à valeurs dans l'ensemble
et
une variable aléatoire telle que, conditionnellement à
,
suit une loi de Bernoulli de paramètre
. Explicitement, on a
et
. Donner la loi et l'espérance de
.
On remarque que, comme les valeurs possibles pour  sont 0 et 1, la loi de
sont 0 et 1, la loi de  sera forcément une loi de Bernoulli ! Il faut calculer son paramètre
sera forcément une loi de Bernoulli ! Il faut calculer son paramètre 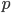 , c'est-à-dire la proba
, c'est-à-dire la proba 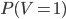 . On a
. On a
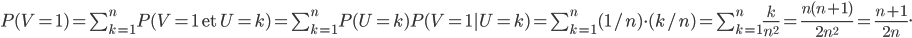
L'espérance de  est très simple à calculer, car on a
est très simple à calculer, car on a 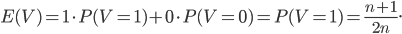
Soit
une variable aléatoire de loi de Poisson de paramètre
. On suppose une variable
telle que conditionnellement à
,
suit une loi binomiale de paramètre
et
. Après avoir donné un sens mathématique à la phrase précédente, montrer que
est une loi de Poisson de paramètre
.
On nous dit que  est une variable aléatoire telle que
est une variable aléatoire telle que 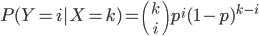 et que
et que  est une variable de Poisson de paramètre
est une variable de Poisson de paramètre 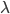 . Pour chaque
. Pour chaque  on a alors
on a alors

Feuille 4 exo 1 – corrigé
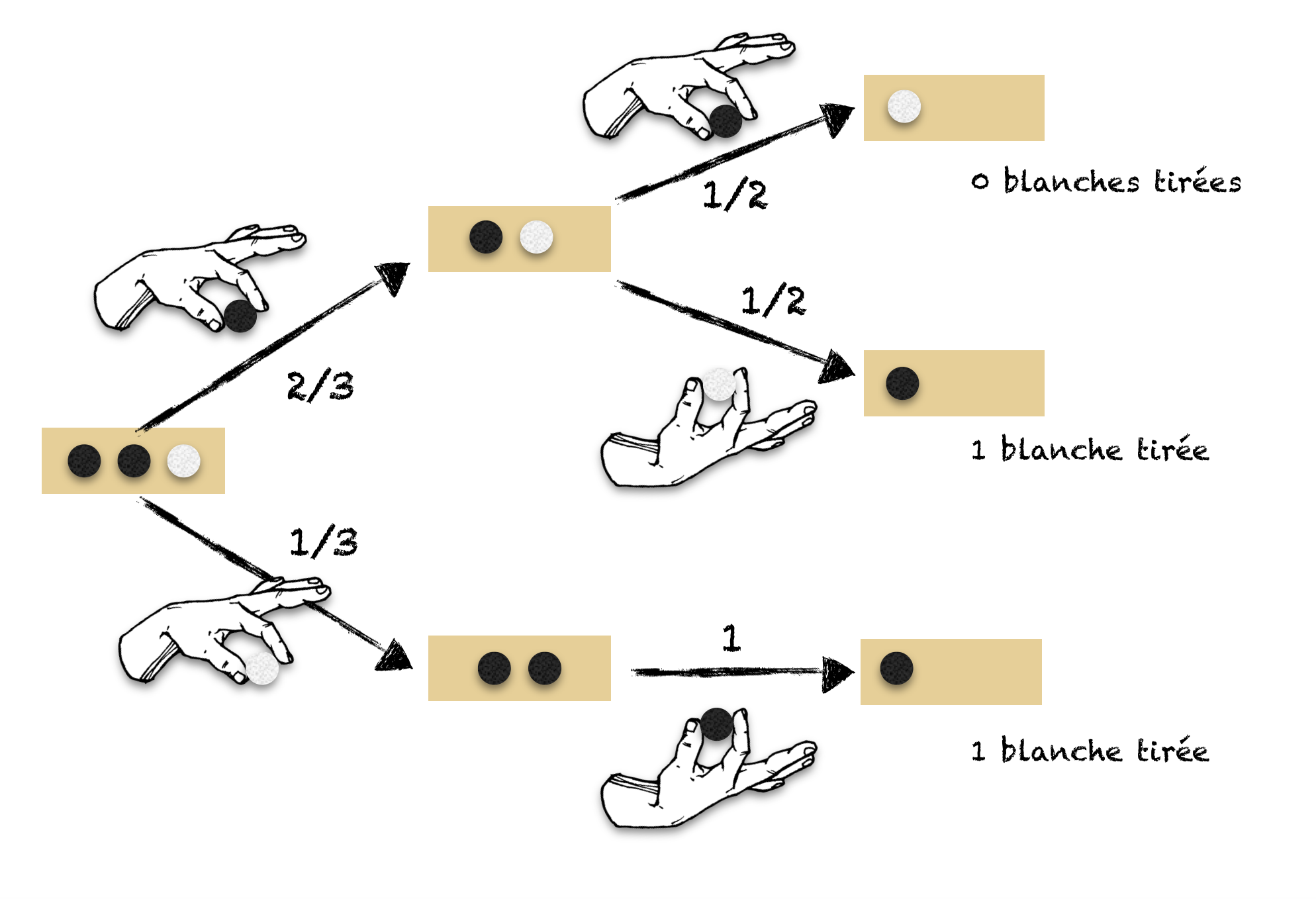
On dispose de 4 boîtes numérotées de 0 à 3. La boîte numéro 3 contient 3 boules blanches, la boîte numéro 2 2 boules blanches et 1 boule noire, la boîte numéro 1 1 boule blanche et 2 boules noires et la boîte numéro 0 3 boules noires. On choisit une boîte au hasard et 2 boules dans cette boîte. Soit
le numéro de la boîte tirée et
le nombre de boules blanches tirées. Trouver la loi de
, puis celle de
. Quel sera le signe de la covariance entre
et
? (On demande un raisonnement et non un calcul.)
Voici une solution détaillée en plusieurs étapes ; essayez de répondre à chaque question vous mêmes avant de lire la réponse !
Quelles sont les valeurs possibles pour  ?
?
Les valeurs possibles sont 0, 1, 2, 3, c’est à dire les nombres associés aux 4 boîtes.
Quelles sont les valeurs possibles pour  ?
?
Il s’agit des valeurs 0, 1, 2 : au minimum on va tirer 0 boules blanches, et au maximum 2 (comme l’expérience consiste à tirer deux boules de l'une des 4 boîtes).
Trouver la loi de 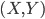 .
.
Il faut remplir une table comme la suivante avec les probabilités que 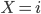 et
et 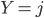 , pour tout couples d'entiers
, pour tout couples d'entiers 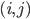 où
où 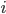 est entre 0 et 3,
est entre 0 et 3, 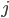 entre 0 et 2.
entre 0 et 2.
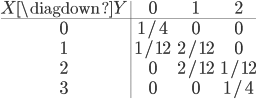
Par exemple, la table dit que 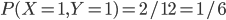 . Mais comment est-ce qu'on l'a remplie ?
. Mais comment est-ce qu'on l'a remplie ?
On va d'abord s'occuper de la première ligne ; on cherche donc 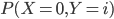 pour
pour 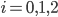 . On sait que
. On sait que 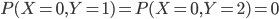 , parce que il n'y a pas de boules blanches dans la boîte 0 (il est donc impossible de choisir la boîte 0 et d'en tirer une ou deux boules blanches). Par contre, on a
, parce que il n'y a pas de boules blanches dans la boîte 0 (il est donc impossible de choisir la boîte 0 et d'en tirer une ou deux boules blanches). Par contre, on a 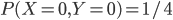 , c'est-à-dire la probabilité de choisir la boîte 0 (après,
, c'est-à-dire la probabilité de choisir la boîte 0 (après, 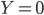 est garanti).
est garanti).
On calcul les probas de la dernière ligne exactement de la même façon : il y a que des boules blanches dans la boîte 3 (on en tirera forcement 2 boules blanches), donc 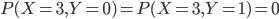 et
et 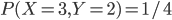 .
.
Pour la deuxième ligne, on veut les probas de choisir la boîte 1 (qui a une boule blanche, deux noires) et en tirer 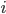 boules blanches (
boules blanches (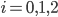 ). Il est assez simple de calculer ces probas directement, mais on va faire un arbre pour mieux clarifier la situation :
). Il est assez simple de calculer ces probas directement, mais on va faire un arbre pour mieux clarifier la situation :
Sachant qu'on a choisit la boîte 1, la proba de tirer 0 boules blanches est 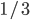 (c'est la proba de tirer deux fois une boule noire) et la proba d'en tirer une est
(c'est la proba de tirer deux fois une boule noire) et la proba d'en tirer une est 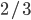 (soit on tire une blanche, puis une noire, soit une noire, puis une blanche). On pourrait aussi faire un raisonnement du type: on tire 0 blanches si la boule qui reste est la blanche (proba 1/3) et exactement une blanche si la boule qui reste est noire (2 chances sur 3). Comme la proba de choisir la boîte 1 est 1/4, on a
(soit on tire une blanche, puis une noire, soit une noire, puis une blanche). On pourrait aussi faire un raisonnement du type: on tire 0 blanches si la boule qui reste est la blanche (proba 1/3) et exactement une blanche si la boule qui reste est noire (2 chances sur 3). Comme la proba de choisir la boîte 1 est 1/4, on a 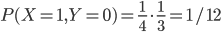 ,
, 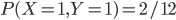 ,
, 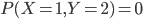 .
.
La situation de la boîte 2 est exactement symétrique.
Quel sera le signe de la covariance ?
Quand  est plus grand, la proba que
est plus grand, la proba que  soit grand augmente, car il y a plus de boules blanches dans les boîtes associées à un nombre plus grand. On s’attend donc une covariance positive.
soit grand augmente, car il y a plus de boules blanches dans les boîtes associées à un nombre plus grand. On s’attend donc une covariance positive.
Essayez de répondre aux questions suivantes pour vous entraîner !
- Calculer la loi de
 .
. - Calculer l'esperance de
 et celle de
et celle de  .
. - Calculer
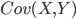 .
.
[Réponses : la loi de  est uniforme sur
est uniforme sur 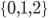 (chaque résultat a proba 1/3) ;
(chaque résultat a proba 1/3) ; 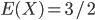 ;
; 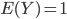 ;
; 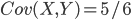 .]
.]
Corrigé Interro 1
Vous trouverez ici un corrigé écrit du premier contrôle préparé par Linxiao.
Contrôle 3 Exo 2 – Corrigé
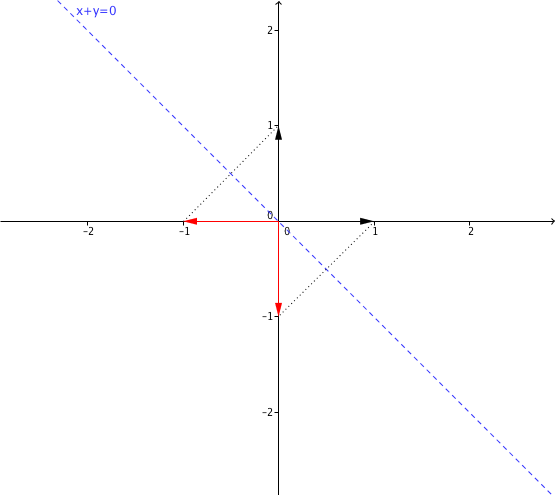
Problème 2. On considère la droite de
d'équation
; soit
l'application linéaire qui à chaque vecteur du plan associe son symétrique par rapport à cette droite.
- Déterminer la matrice
associée à l'application
par rapport à la base canonique de
(au départ et à l'arrivée).
Soit 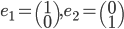 la base canonique de
la base canonique de  . Les colonnes de la matrice
. Les colonnes de la matrice 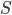 sont les vecteurs
sont les vecteurs 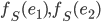 (exprimés dans la base canonique), donc on a simplement
(exprimés dans la base canonique), donc on a simplement
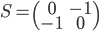 .
.
- Montrer que la matrice
(c'est-à-dire le produit entre la matrice
et elle même) est la matrice identité.
On a bien  .
.
- On considère la matrice
; quel est le noyau de l'application linéaire
correspondante ? Quelle est son image ?
On a
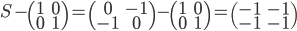
L'application linéaire  correspondante a comme image l'espace engendré par les colonnes de cette matrice, c'est-à-dire la droite engendrée par
correspondante a comme image l'espace engendré par les colonnes de cette matrice, c'est-à-dire la droite engendrée par 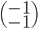 (autrement dit, la droite
(autrement dit, la droite 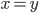 ).
).
Le noyau de 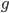 est l'ensemble des vecteurs
est l'ensemble des vecteurs 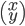 tels que
tels que 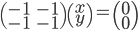 , c'est à dire tels que
, c'est à dire tels que 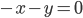 . Il s'agit donc de la droite
. Il s'agit donc de la droite 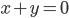 par rapport à laquelle on avait pris les symétriques.
par rapport à laquelle on avait pris les symétriques.
- Montrer que tout vecteur de
est orthogonale à tout vecteur de l'image de
.
Un vecteur de 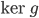 est de la forme
est de la forme 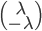 et un vecteur de l'image de
et un vecteur de l'image de 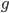 de la forme
de la forme 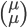 . Leur produit scalaire est
. Leur produit scalaire est  .
.
- Déterminer la matrice associée à
par rapport à la base
(au départ et à l'arrivée).
Les colonnes de la matrices sont les images des vecteurs donnés, exprimées en coordonnées par rapport à la base 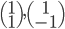 , que l'on va appeler
, que l'on va appeler 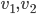 .
.
On a 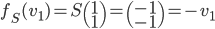 ; les coordonnées de
; les coordonnées de 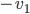 par rapport à la base
par rapport à la base 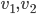 sont
sont 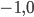 , donc la première colonne de la matrice sera
, donc la première colonne de la matrice sera 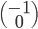 . On a
. On a 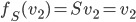 , qui a coordonnées
, qui a coordonnées 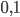 . La matrice cherchée est donc
. La matrice cherchée est donc 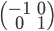 .
.
On sait que l'application linéaire
qui à chaque vecteur du plan associe son image par une rotation d'un angle
autour de l'origine est représentée par la matrice
(par rapport à la base canonique).
- Montrer que pour tout
et tout
le vecteur
a la même norme que le vecteur
.
Soit 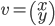 , alors
, alors 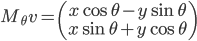 ; la norme de
; la norme de 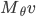 est la racine carrée de
est la racine carrée de 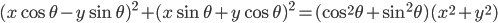 . Comme pour tout
. Comme pour tout 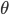
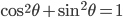 , la norme de
, la norme de 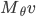 est
est 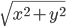 , c'est-à-dire la norme de
, c'est-à-dire la norme de 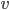 .
.
- Montrer que pour tout
on a
.
Remarquez que ça revient à dire que symétriser par rapport à la droite 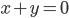 , faire une rotation de
, faire une rotation de 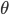 et puis symétriser encore une fois donne le même résultat que faire seulement une rotation de
et puis symétriser encore une fois donne le même résultat que faire seulement une rotation de 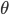 dans le sens inverse, ce qui se voit bien géométriquement.
dans le sens inverse, ce qui se voit bien géométriquement.
On peut aussi faire le calcul: on a

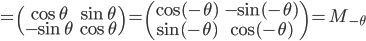 .
.
- Montrer que pour tout
on a
.
On a montré que 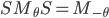 , donc
, donc 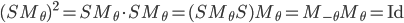 .
.
La dernière égalité est claire du point de vue des applications linéaire correspondantes, qui sont l'une l'inverse de l'autre, mais peut aussi être montrée en faisant les calcul du produit matriciel.
Contrôle 3 Exo 1 – Corrigé
Problème 1. Soient
et
les espaces vectoriels suivants :
- Quelle est la dimension de
?
L'espace  est défini comme sous-espace de
est défini comme sous-espace de 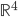 par une seule équation, donc sa dimension est
par une seule équation, donc sa dimension est 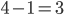 .
.
- Exprimer
comme le noyau d'une application linéaire entre
et $\mathbb{R}^2$. En déduire la dimension de
.
L'espace 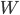 est le noyau de l'application linéaire
est le noyau de l'application linéaire 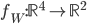 représentée (par rapport aux bases canoniques de
représentée (par rapport aux bases canoniques de 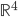 et
et  ) par la matrice
) par la matrice
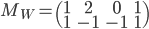 .
.
On a 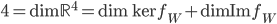 ; l'image de
; l'image de 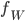 , qui est engendrée par les colonnes de la matrice
, qui est engendrée par les colonnes de la matrice 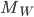 , est incluse dans
, est incluse dans  et contient deux vecteurs non-colinéaires (par exemple les deux premières colonnes de la matrice
et contient deux vecteurs non-colinéaires (par exemple les deux premières colonnes de la matrice 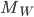 ) donc a dimension 2.
) donc a dimension 2.
Finalement, 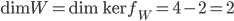 .
.
On considère les familles de vecteurs suivantes :
- Montrer que
est une base de
, et que
est une base de
.
Les vecteurs 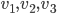 sont trois vecteurs libres (
sont trois vecteurs libres (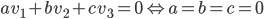 ) de
) de  (car leur coordonnées satisfont à l'équation
(car leur coordonnées satisfont à l'équation 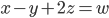 ). La dimension de
). La dimension de  est trois, donc
est trois, donc 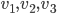 est une base de
est une base de  .
.
De même pour 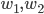 . Je ne vais pas écrire plus de détails, parce que essentiellement tout le monde a réussi cette question. Bravo !
. Je ne vais pas écrire plus de détails, parce que essentiellement tout le monde a réussi cette question. Bravo !
- Existe-t-il une application linéaire de
vers
dont le noyau est
?
Non ! Une application linéaire  de
de  vers
vers 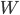 est toujours telle que
est toujours telle que 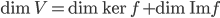 . Par contre, on sait que
. Par contre, on sait que 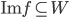 , donc
, donc 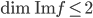 , dont on obtient
, dont on obtient 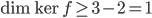 ; la dimension du noyau de
; la dimension du noyau de  est au moins 1, donc le noyau ne peut dans aucun cas être
est au moins 1, donc le noyau ne peut dans aucun cas être 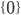 .
.
- Montrer qu'il existe une unique application linéaire
telle que
Existence et unicité sont une conséquence du fait que 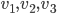 forment une base de
forment une base de  , et que les vecteurs
, et que les vecteurs 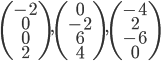 appartiennent à
appartiennent à 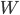 .
.
- Quelle est la matrice associée à
par rapport aux bases
et
?
Les colonnes de 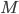 contiennent les coordonnées des vecteurs
contiennent les coordonnées des vecteurs 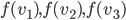 par rapport à la base
par rapport à la base 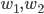 . En faisant les calculs, on obtient
. En faisant les calculs, on obtient
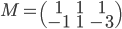 .
.
- Calculer
(exprimer le résultat comme un vecteur de
).
On a 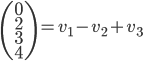 , donc
, donc  .
.
On pourrait aussi calculer 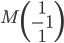 (où
(où 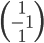 est le vecteur des coordonnées de
est le vecteur des coordonnées de 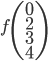 par rapport à la base
par rapport à la base 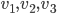 ), ce qui nous donne le vecteur
), ce qui nous donne le vecteur 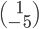 . On a donc
. On a donc 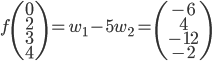 .
.
- Quelle est la dimension de
? En déduire la dimension de
.
On sait que 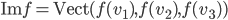 ; on sait aussi que
; on sait aussi que 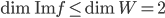 . Comme les vecteurs
. Comme les vecteurs 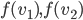 ne sont pas colinéaires, on déduit que
ne sont pas colinéaires, on déduit que 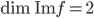 .
.
Par conséquence, on a 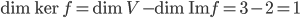 .
.
- Déterminer une base de
(on exprimera les éléments de cette base comme vecteurs de
).
On a que 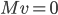 pour un vecteur
pour un vecteur 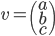 si et seulement si
si et seulement si 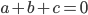 et
et 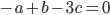 , c'est-à-dire pour les vecteurs
, c'est-à-dire pour les vecteurs 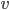 de la forme
de la forme 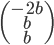 .
.
Les vecteurs du noyau de  sont donc ceux qui s'écrivent sous la forme
sont donc ceux qui s'écrivent sous la forme 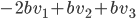 ; en posant
; en posant 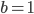 on trouve que le vecteur
on trouve que le vecteur 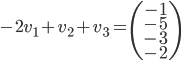 forme une base de
forme une base de 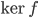 .
.