PeiPC Maths – Semaine 1

Séance 1 – 3/11

• Équations des droites dans le plan
• La droite passante par deux points
• Droites parallèles
• Droites orthogonales
• La droite orthogonale à une droite d’équation donnée passante par un point donné

QUESTIONS:

• Donner une équation de la droite passante par 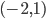$(-2,1)$ et $(3,2)$.
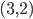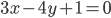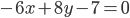• Est-ce que les droites définies par $3x-4y+1=0$ et $-6x+8y-7=0$ sont parallèles ?
• Déterminer une équation de la droite orthogonale à la droite d’équation 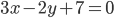$3x-2y+7=0$ et passante par l’origine.
• Déterminer une équation de la droite orthogonale à la droite d’équation 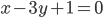$x-3y+1=0$ et passante par $(2,3)$.

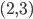Séance 2 – 4/11

• La distance entre un point et une droite (calcul en coordonnées)
• Équations des cercles dans le plan
• Déterminer centre et rayon d’un cercle à partir de son équation
• La droite tangente à un cercle en un point donné
• Vecteurs dans le plan: somme, différence, introduction au produit scalaire

QUESTIONS:

• Quelle est la distance entre la droite d'équation 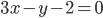$3x-y-2=0$ et le point $(1,2)$ ?
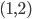• Quelles sont les coordonnées du centre du cercle d’équation 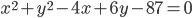$x^2+y^2-4x+6y-87=0$ ? Quel est son rayon ?
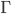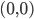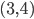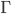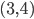• Soit $\Gamma$ le cercle de centre $(0,0)$ passant par le point $(3,4)$. Déterminer une équation de la droite tangente à $\Gamma$ en $(3,4)$. Quel est le rayon du cercle ?
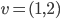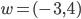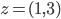• On considère les vecteurs $v=(1,2)$, $w=(-3,4)$ et $z=(1,3)$. Déterminer le produit scalaire entre le vecteur 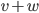$v+w$ et le vecteur $z-v$. Calculer la norme (c'est-à-dire la longueur) du vecteur $v+w-z$.

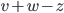Séance 3 – 5/11

• Produit scalaire de vecteurs dans le plan: projections, norme, angles
• Équation d’une droite donnée en termes d’un produit scalaire: trouver un vecteur normal
• Produit scalaire et rotations
• Distance d’une droite de l’origine
• Distance entre un point donné et une droite donnée en utilisant les produits scalaires

QUESTIONS:

• Dessiner le lieu des points 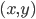$(x,y)$ tels que 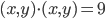$(x,y)\cdot (x,y)=9$ dans le plan.
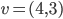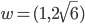• Soient $v=(4,3)$ et $w=(1,2\sqrt{6})$ ; quel est l’angle entre 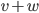$v+w$ et $v-w$ ?
• Déterminer les coordonnées d’un vecteur de longueur 1 orthogonal à la droite d’équation $5x-12y-7=0$.
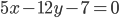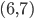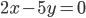• Déterminer la distance entre le point $(6,7)$ et la droite d’équation $2x-5y=0$.