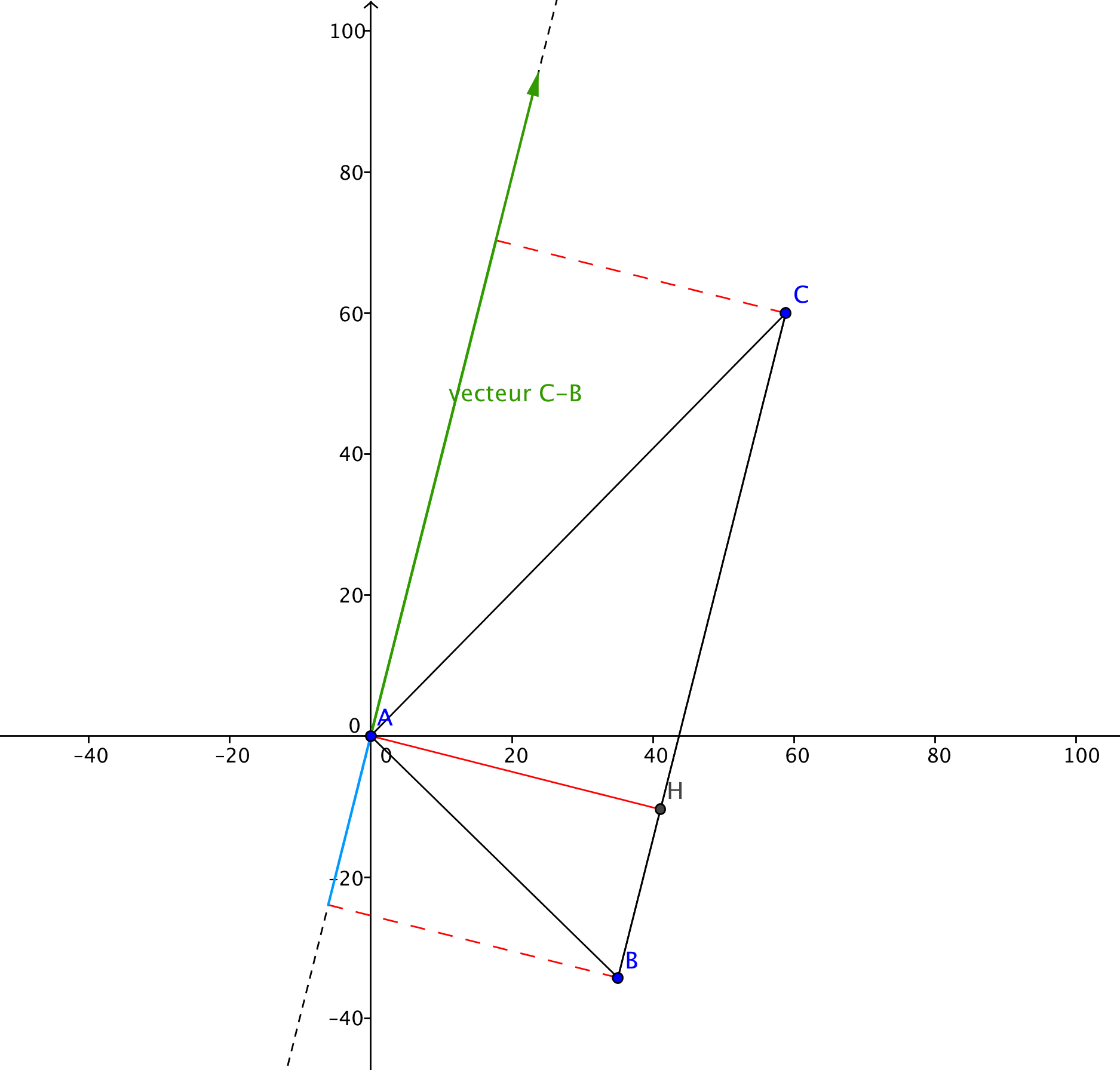
On considère les points
,
,
de coordonnées
,
et
. Montrer que le triangle
est rectangle. Soit
le pied de la hauteur issue du point
; sans calculer les coordonnées de
, déterminer les longueurs des segments
,
et
(on pourra inverser la relation
pour l'aire d'un triangle). Vérifier la relation
(théorème d'Euclide).
1 - Le triangle ABC est rectangle
Je vais montrer que le triangle 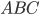 est rectangle en
est rectangle en 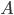 , c'est-à-dire que les vecteurs
, c'est-à-dire que les vecteurs 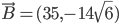 et
et 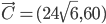 sont orthogonaux.
sont orthogonaux.
Cela revient à vérifier que le produit scalaire 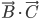 est nul, et en effet
est nul, et en effet
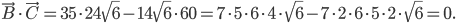
Remarques : une autre manière de montrer qu'un triangle est rectangle est de vérifier la relation du théorème de Pythagore, c'est-à-dire dans notre cas le fait que 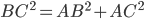 ; ça comporte plus de calculs, mais comme on aura besoin des longueurs des trois côtés plus tard, ce n'est pas forcément une mauvaise idée de les calculer au tout début de l'exo.
; ça comporte plus de calculs, mais comme on aura besoin des longueurs des trois côtés plus tard, ce n'est pas forcément une mauvaise idée de les calculer au tout début de l'exo.
2 - Les projections BH et CH comme fonctions des côtés du triangle
Les segments 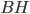 et
et 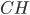 sont les projections des segments
sont les projections des segments 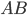 et
et 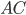 le long de
le long de 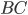 . Étant donné un vecteur
. Étant donné un vecteur 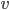 parallèle à
parallèle à 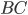 , on peut donc calculer leur longueurs comme
, on peut donc calculer leur longueurs comme 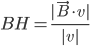 et
et 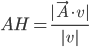 .
.
Le vecteur  est bien parallèle au côté
est bien parallèle au côté 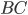 du triangle, ce qui implique par exemple
du triangle, ce qui implique par exemple 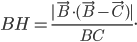
Mais 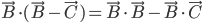 ; de plus, on a déjà montré que
; de plus, on a déjà montré que 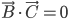 (les deux sont orthogonaux) et on sait que
(les deux sont orthogonaux) et on sait que 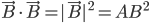 (le produit scalaire entre un vecteur et soi-même, comme l'angle est nul, est la norme au carré).
(le produit scalaire entre un vecteur et soi-même, comme l'angle est nul, est la norme au carré).
On a donc 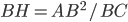 .
.
De même, 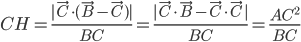 .
.
Remarques : comme on sait qu'on va devoir calculer la longueur de 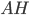 , on pourrait aussi utiliser le théorème de Pythagore pour exprimer
, on pourrait aussi utiliser le théorème de Pythagore pour exprimer 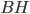 et
et 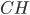 comme
comme 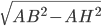 et
et 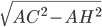 . Je vous donne une solution qui utilise les produits scalaire pour que vous vous habituez à les utiliser dans le calcul de la longueur d'une projection. Il est important de comprendre le raisonnement qui est ci-dessus.
. Je vous donne une solution qui utilise les produits scalaire pour que vous vous habituez à les utiliser dans le calcul de la longueur d'une projection. Il est important de comprendre le raisonnement qui est ci-dessus.
3 - Une expression pour 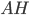 et l'identité d'Euclide
et l'identité d'Euclide
En même temps, on peut calculer 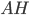 grâce aux deux expressions pour l'aire du triangle, qui vaut
grâce aux deux expressions pour l'aire du triangle, qui vaut 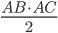 aussi bien que
aussi bien que 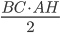 ; on a donc l'identité
; on a donc l'identité 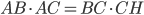 , et finalement
, et finalement 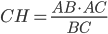 .
.
Remarquez qu'avec ça on a l'identité cherchée, même sans faire les calculs !
En effet, on a trouvé 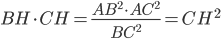 .
.
4 - Calculs
Pour trouver les valeurs des longueurs, il suffit de faire des petits calculs : on a
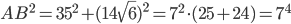
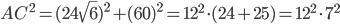
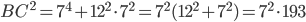
Finalement, on trouve
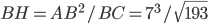
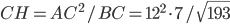
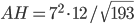
Remarques : oui, je me suis trompée : j'avais l'intention de créer un calcul un peu plus joli. Mais une racine de quelque chose ne doit pas vous gêner ! Quand vous avez un calcul à faire, substituez les valeurs numériques aussi tard que possible : les parties 2 et 3 de cet exo sont bien plus simples à écrire, et bien plus intéressantes, sans des nombre compliqués qui peuvent nous distraire de ce que nous sommes en train de faire. Quand on arrive au calcul lui-même, il est mieux de factoriser ce qu'il y a sous les racines et de sortir les carrés, sans utiliser la calculette ; vous pouvez tout simplement laisser la racine dans le résultat !