Problème 7. On considère les vecteurs
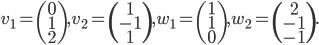
Soient 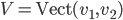 et
et 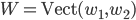 . Déterminer une base de
. Déterminer une base de  . Quelle est la dimension de l'espace engendré par
. Quelle est la dimension de l'espace engendré par  et
et 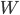 ?
?
Un vecteur de 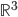 appartient à
appartient à  si et seulement si il est à la fois une combinaison linéaire de
si et seulement si il est à la fois une combinaison linéaire de 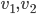 et une combinaison linéaire de
et une combinaison linéaire de 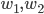 , c'est-à-dire
, c'est-à-dire 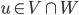 si et seulement s'il existe
si et seulement s'il existe 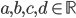 tels que
tels que
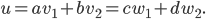
On cherche donc 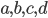 tels que
tels que
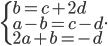
En utilisant la première equation et la deuxième, on obtient 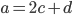 , d'où (3ème equation)
, d'où (3ème equation) 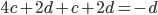 , et donc
, et donc 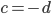 . On a ainsi
. On a ainsi 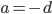 ,
, 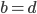 ,
, 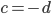 , et donc finalement les vecteurs dans
, et donc finalement les vecteurs dans  sont tous de la forme
sont tous de la forme
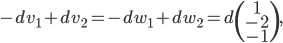
pour 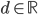 . L'espace
. L'espace  est donc la droite engendrée par le vecteur
est donc la droite engendrée par le vecteur 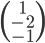 (qui est bien une base de la droite elle-même).
(qui est bien une base de la droite elle-même).
Comme on a montré que  , la formule de Grassmann nous assure que
, la formule de Grassmann nous assure que
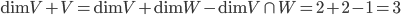 ,
,
donc que l'espace engendré par  et
et 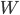 est bien
est bien 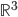 .
.


