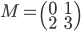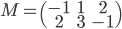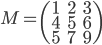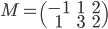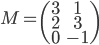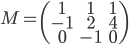Applications linéaires et matrices
QUESTIONS :
[♠︎❄︎] Pour chaque couple (matrice 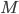 , vecteur
, vecteur 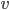 ) dire si le produit matrice par vecteur
) dire si le produit matrice par vecteur 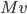 a un sens et, dans ce cas, le calculer.
a un sens et, dans ce cas, le calculer.
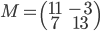 ,
, 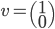
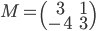 ,
, 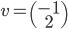
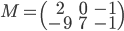 ,
, 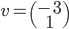
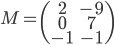 ,
, 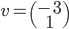
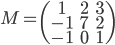 ,
, 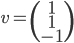
[♠︎❄︎] Pour chaque couple de matrices 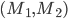 dire si le produit matriciel
dire si le produit matriciel 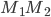 a un sens et, dans ce cas, le calculer.
a un sens et, dans ce cas, le calculer.
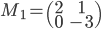 ,
, 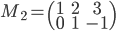
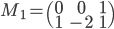 ,
, 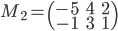
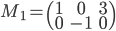 ,
, 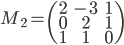
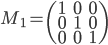 ,
, 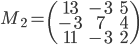 (que remarquez-vous ? Auriez-vous pu prédire le résultat ?)
(que remarquez-vous ? Auriez-vous pu prédire le résultat ?)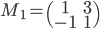 ,
, 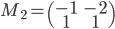
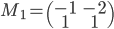 ,
, 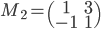 (que remarquez-vous par rapport à la question précédente ?)
(que remarquez-vous par rapport à la question précédente ?)
[♠︎❄︎] Pour chacune des matrices 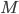 suivantes, soit
suivantes, soit  l'unique application linéaire de
l'unique application linéaire de 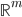 vers
vers 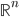 représentée par
représentée par 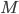 (dans les bases canoniques). Dans chaque cas, préciser
(dans les bases canoniques). Dans chaque cas, préciser 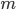 et
et 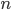 , et calculer
, et calculer 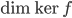 et
et 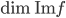 . Quand
. Quand 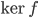 est non trivial, en déterminer une base.
est non trivial, en déterminer une base.