Soit
une variable aléatoire de loi uniforme sur
. Soit
une variable al\'eatoire de loi uniforme sur
. Donner un sens mathématique à la phrase précédente ; donner la loi de
, et calculer l'espérance de
en fonction de
.
On sait que, quand 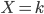 , "la variable
, "la variable 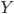 est uniforme sur
est uniforme sur  ", ce qui veut dire que pour
", ce qui veut dire que pour 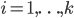 , on a
, on a 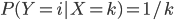 .
.
Les valeurs possibles de 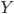 sont
sont 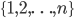 , et pour calculer
, et pour calculer 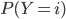 (
(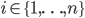 ) il faut d'abord distinguer les cas possibles pour la valeur de
) il faut d'abord distinguer les cas possibles pour la valeur de 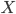 . On a
. On a
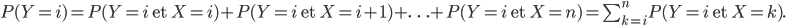
Mais 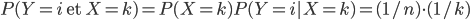 (si
(si 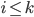 ) et donc
) et donc
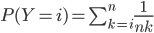 .
.
On a alors 
Soit
une variable aléatoire de loi uniforme à valeurs dans l'ensemble
et
une variable aléatoire telle que, conditionnellement à
,
suit une loi de Bernoulli de paramètre
. Explicitement, on a
et
. Donner la loi et l'espérance de
.
On remarque que, comme les valeurs possibles pour 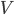 sont 0 et 1, la loi de
sont 0 et 1, la loi de 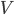 sera forcément une loi de Bernoulli ! Il faut calculer son paramètre
sera forcément une loi de Bernoulli ! Il faut calculer son paramètre 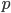 , c'est-à-dire la proba
, c'est-à-dire la proba 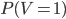 . On a
. On a
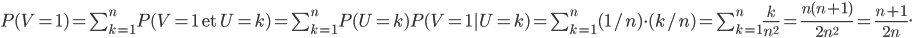
L'espérance de 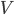 est très simple à calculer, car on a
est très simple à calculer, car on a 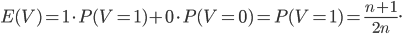
Soit
une variable aléatoire de loi de Poisson de paramètre
. On suppose une variable
telle que conditionnellement à
,
suit une loi binomiale de paramètre
et
. Après avoir donné un sens mathématique à la phrase précédente, montrer que
est une loi de Poisson de paramètre
.
On nous dit que 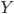 est une variable aléatoire telle que
est une variable aléatoire telle que 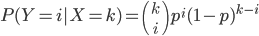 et que
et que 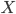 est une variable de Poisson de paramètre
est une variable de Poisson de paramètre 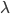 . Pour chaque
. Pour chaque  on a alors
on a alors



