Chiusure, parti interne, frontiere, palle in 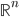
1. [Svolto 2/2] Che relazioni di contenimento esistono fra  e
e  , fra
, fra  e
e  , fra
, fra  e
e 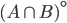 , fra
, fra  e
e 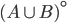 ? (Quando una relazione di contenimento non è vera in generale, fornire un controesempio.)
? (Quando una relazione di contenimento non è vera in generale, fornire un controesempio.)
2. [Svolto 2/2] Che relazioni di contenimento esistono fra 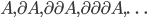 ? (Quando una relazione di contenimento non è vera in generale, fornire un controesempio.)
? (Quando una relazione di contenimento non è vera in generale, fornire un controesempio.)
3. [Svolto 2/2] Dimostrare che ogni aperto di  è un'unione disgiunta numerabile di intervalli aperti (i.e. intervalli della forma
è un'unione disgiunta numerabile di intervalli aperti (i.e. intervalli della forma 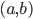 , con
, con 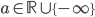 e
e 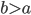 in
in 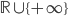 ).
).
4. [Svolto 2/2] È vero che ogni aperto di 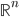 è unione numerabile di palle aperte? È vero che ogni aperto di
è unione numerabile di palle aperte? È vero che ogni aperto di 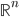 è unione di palle aperte disgiunte?
è unione di palle aperte disgiunte?
5. [Svolto 9/2] Quali sono i sottoinsiemi di  che sono sia chiusi sia aperti? E quelli di
che sono sia chiusi sia aperti? E quelli di 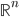 ?
?
6. Si può esprimere 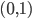 come unione numerabile di intervalli chiusi disgiunti?
come unione numerabile di intervalli chiusi disgiunti?
Una digressione sulla dimensione di Minkowski
Dato un insieme 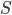 limitato in
limitato in 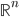 e dato
e dato 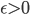 , definiamo
, definiamo 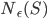 come il minimo
come il minimo 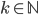 tale che esistano
tale che esistano 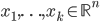 per cui
per cui 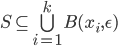 , i.e. il minimo numero di palle aperte di
, i.e. il minimo numero di palle aperte di 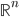 sufficiente per coprire l'insieme
sufficiente per coprire l'insieme 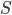 . Definiamo la dimensione di Minkowski superiore di
. Definiamo la dimensione di Minkowski superiore di 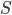 come
come
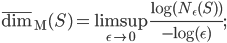
similmente si definisce la dimensione di Minkowski inferiore come il 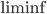 corrispondente e, se le due coincidono, il loro valore è detto semplicemente dimensione di Minkowski e denotato con
corrispondente e, se le due coincidono, il loro valore è detto semplicemente dimensione di Minkowski e denotato con 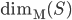 .
.
7. [Svolto 2/2] Mostrare che, per ![S=[0,1]^d\times \{0\}^{n-d}](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_a988b33b3042128d545525007712dbe6.gif) , con
, con 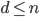 , si ha
, si ha 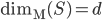 .
.
8. [Svolto 2/2] Mostrare che, per ![(S=[0,1]\cap\mathbb{Q})\times \{0\}^{n-1}](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_d9d29590cba9ddc8a3dda077d4544bd9.gif) , si ha
, si ha 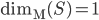 .
.
9. Mostrare le seguenti proprietà (enunciate per la dimensione superiore, ma valide anche per quella inferiore):
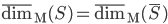 ;
;- se
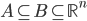 ,
, 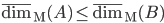 ;
; 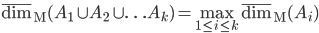 (cosa si può dire nel caso di un'unione numerabile?);
(cosa si può dire nel caso di un'unione numerabile?);- Se
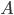 è finito, allora
è finito, allora 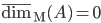 .
.
10. Dato  limitato ed
limitato ed 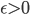 , definiamo le seguenti quantità:
, definiamo le seguenti quantità:
![N^{box}_\epsilon(S)=\min\{k\mid \exists x_1,\ldots, x_k\in\mathbb{R}^n : S\subseteq \bigcup_{i=1}^k x_i+[-\epsilon/2,\epsilon/2]^n\}](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_52631e50e19e14ed164699ccec509e64.gif)
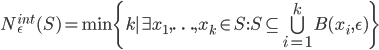
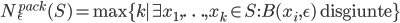
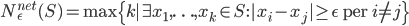
Mostrare che la dimensione di Minkowski (superiore/inferiore) si può definire equivalentemente con qualunque di queste quantità al posto di 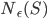 .
.
11. Calcolare 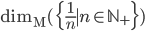 .
.
12. Calcolare 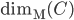 , dove
, dove ![C\subset [0,1]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_9d9b63f05877e2fd091ca6df4f6eb2a1.gif) è l'insieme di Cantor.
è l'insieme di Cantor.
13. Produrre un esempio di insieme 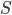 per il quale la dimensione di Minkowski superiore e quella inferiore non coincidono.
per il quale la dimensione di Minkowski superiore e quella inferiore non coincidono.
14. Calcolare ![\operatorname{dim_M}(\{(x,\sin(1/x))\mid x\in (0,1]\})](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_c574b22a4525b42a7b6f267ea15f9120.gif) .
.
15. Dimostrare che, se  è una funzione reale
è una funzione reale 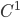 su
su ![[0,1]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_ccfcd347d0bf65dc77afe01a3306a96b.gif) , allora il suo grafico
, allora il suo grafico ![\{(x,f(x))\mid x\in[0,1]\}\subset \mathbb{R}^2](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_6b62670e3075da92e5d5da27ab38b49c.gif) ha dimensione di Minkowski 1. Riuscite ad indebolire la condizione
ha dimensione di Minkowski 1. Riuscite ad indebolire la condizione 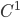 ? In particolare, lo statement è vero per una funzione continua?
? In particolare, lo statement è vero per una funzione continua?


