Curve
71. Disegnare una rappresentazione approssimativa delle seguenti curve in  e calcolarne la lunghezza in funzione del parametro
e calcolarne la lunghezza in funzione del parametro 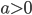 :
:
- (Astroide)
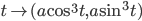 , per
, per ![t\in[0,2\pi]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_fe633d652f3e72a8166a95d781b83845.gif) ;
; - (Cardioide) l'insieme dei punti della forma
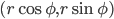 , dove
, dove 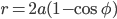 .
.
72. Dimostrare che la lunghezza dell'ellisse  (con
(con 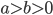 ,
, ![\phi\in[0,2\pi]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_fe24cdb8673de5158ebce2610614cdbe.gif) ) è
) è 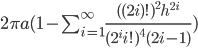 , con
, con 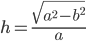 .
.
73. Dati 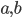 reali positivi, definiamo le due successioni
reali positivi, definiamo le due successioni 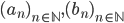 ponendo
ponendo 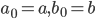 ,
, 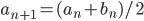 ,
, 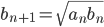 . Mostrare che le due successioni tendono allo stesso limite finito e positivo, che chiameremo
. Mostrare che le due successioni tendono allo stesso limite finito e positivo, che chiameremo 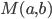 .
.
74. Dimostrare che, dati 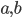 reali positivi e detto
reali positivi e detto 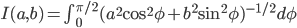 , vale
, vale 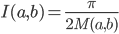 , con la notazione dell'esercizio precedente. Hint: con un cambio di coordinate, dimostrare che
, con la notazione dell'esercizio precedente. Hint: con un cambio di coordinate, dimostrare che 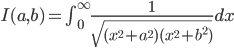 .
.
75. Disegnare la Lemniscata di Bernoulli, cioè l'insieme dei punti 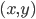 del piano tali che
del piano tali che 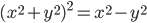 . Mostrare che si tratta di una curva la cui lunghezza totale è
. Mostrare che si tratta di una curva la cui lunghezza totale è 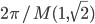 .
.
Teorema della funzione implicita
☞ 76. Sia 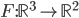 data da
data da 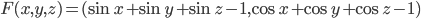 . Sia
. Sia 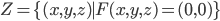 . Mostrare che
. Mostrare che 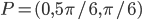 è in
è in 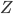 e che esistono funzioni reali
e che esistono funzioni reali 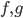 tali che
tali che 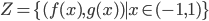 in un intorno di
in un intorno di 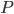 . Scrivere equazioni per la retta tangente a
. Scrivere equazioni per la retta tangente a 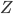 in
in 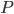 .
.
77. Dato un sottoinsieme 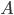 di
di 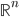 , dimostrare che le seguenti condizioni sono equivalenti:
, dimostrare che le seguenti condizioni sono equivalenti:
- è localmente diffeomorfo a un aperto di 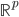 ;
;
- è localmente il grafico di una funzione liscia che esprime 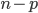 delle coordinate in funzione delle altre
delle coordinate in funzione delle altre 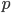 ;
;
- è localmente la controimmagine di 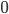 per una funzione da
per una funzione da 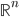 a
a 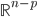 il cui differenziale in
il cui differenziale in 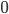 abbia rango
abbia rango 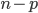 ;
;
- è localmente l'immagine di una funzione liscia da 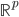 in
in 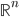 il cui differenziale abbia rango massimo.
il cui differenziale abbia rango massimo.
78. Sia 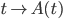 una funzione
una funzione 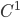 da
da  nelle matrici simmetriche
nelle matrici simmetriche 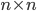 , considerate nello spazio euclideo
, considerate nello spazio euclideo 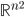 . Supponiamo che
. Supponiamo che 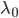 sia un autovalore di
sia un autovalore di 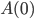 di molteplicità 1. Dimostrare che esistono
di molteplicità 1. Dimostrare che esistono 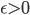 e una funzione
e una funzione 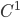
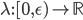 con
con 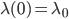 tali che
tali che 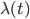 sia un autovalore di
sia un autovalore di 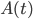 di molteplicità 1 per
di molteplicità 1 per 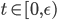 . Dimostrare che
. Dimostrare che 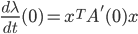 , dove
, dove 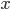 è un autovettore di
è un autovettore di 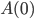 relativo a
relativo a 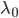 di norma Euclidea uguale a
di norma Euclidea uguale a  .
.
79. Sia 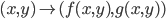 una funzione
una funzione 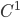 da
da  in sé. Mostrare che localmente una fra
in sé. Mostrare che localmente una fra  e
e 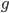 è funzione dell'altra (si può scrivere
è funzione dell'altra (si può scrivere 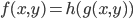 o
o 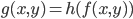 in un appropriato intorno di
in un appropriato intorno di 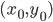 ).
).
80. Sia 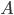 un aperto di
un aperto di  contenente il punto
contenente il punto 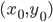 e sia
e sia 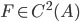 una funzione tale che
una funzione tale che 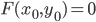 ,
, 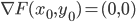 ,
, 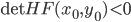 . Sia inoltre
. Sia inoltre 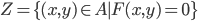 . Dimostrare che, per un opportuno intorno
. Dimostrare che, per un opportuno intorno 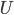 di
di 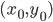 ,
,  è l'unione di due grafici di funzioni
è l'unione di due grafici di funzioni 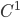 che si intersecano trasversalmente (i.e. che hanno tangenti non coincidenti in
che si intersecano trasversalmente (i.e. che hanno tangenti non coincidenti in 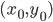 ). Di conseguenza,
). Di conseguenza, 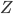 non è localmente il grafico di una funzione in una variabile intorno a
non è localmente il grafico di una funzione in una variabile intorno a 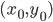 .
.
Moltiplicatori di Lagrange
81. Siano 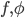 funzioni reali
funzioni reali 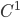 su un aperto
su un aperto 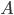 di
di 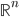 . Dato
. Dato  , sia
, sia 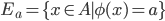 e si supponga
e si supponga 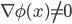 per
per 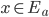 . Mostrare che, se
. Mostrare che, se 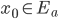 è tale che
è tale che 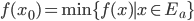 , allora esiste
, allora esiste 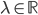 tale che
tale che 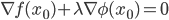 .
.
82. Siano 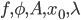 come nell'esercizio precedente, e assumiamo che
come nell'esercizio precedente, e assumiamo che 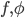 siano
siano 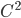 . Sia
. Sia 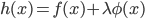 ; mostrare che se
; mostrare che se 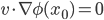 allora
allora 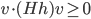 , dove
, dove 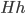 è l'Hessiana di
è l'Hessiana di 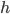 in
in 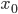 .
.
Ecco una traccia (in verità abbastanza dettagliata) di soluzione per gli ultimi due problemi, che non avevamo corretto per bene a esercitazione; notare che questa soluzione non è la più rapida che si possa produrre, ma è completamente elementare! Moltiplicatori di Lagrange


