Induzione transfinita. Data una proprietà 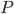 , se per ogni ordinale
, se per ogni ordinale  si ha
si ha
se per ogni ordinale 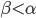 vale
vale 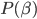 allora vale
allora vale 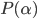
allora la proprietà 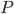 vale per tutti gli ordinali.
vale per tutti gli ordinali.
Esercizi
- Costruire una base di
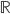 su
su 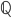 per induzione transfinita.
per induzione transfinita. - Dimostrare che esiste un insieme
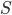 di punti del piano
di punti del piano  tali che ogni retta nel piano contenga esattamente due punti di
tali che ogni retta nel piano contenga esattamente due punti di 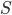 .
. - Dimostrare che esiste una funzione
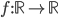 che non sia monotona su nessun sottoinsieme di
che non sia monotona su nessun sottoinsieme di 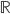 della cardinalità del continuo.
della cardinalità del continuo. - Dimostrare che ogni funzione da
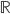 in
in 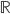 si scrive come somma di due bigezioni da
si scrive come somma di due bigezioni da 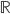 in
in 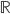 .
.



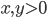
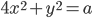
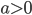
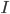
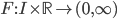
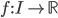
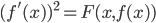
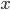
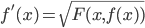
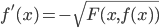
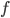
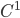
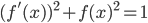
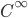
![f:[0,1]\to\mathbb{R}](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_2f88c23f13b9b1904c39f298cd688669.gif)
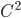
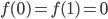
![x\in [0,1]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_c628ba2b1047de93f66cb815d986e107.gif)
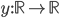
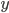
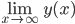
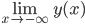
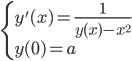
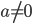
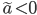
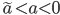
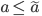

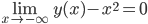
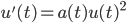
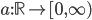
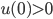
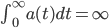
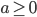
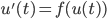
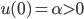
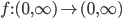
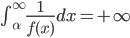
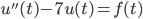
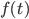
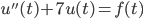
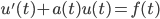
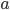
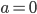
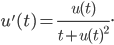
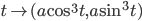
![t\in[0,2\pi]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_fe633d652f3e72a8166a95d781b83845.gif)
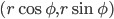
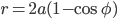

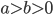
![\phi\in[0,2\pi]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_fe24cdb8673de5158ebce2610614cdbe.gif)
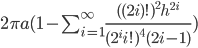
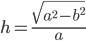
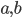
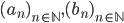
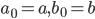
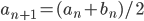
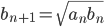
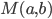
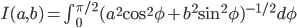
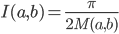
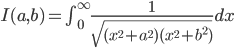
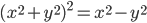
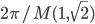
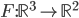
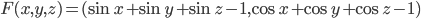
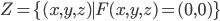
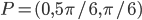
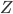
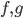
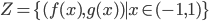
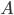
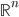
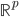
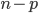
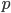
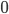
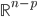
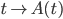
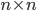
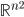
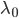
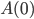
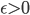
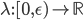
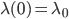
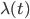
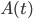
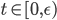
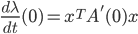

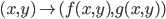
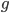
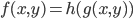
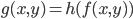
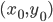
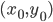
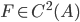
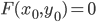
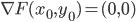
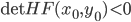
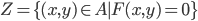
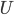

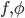

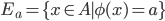
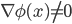
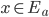
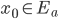
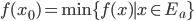
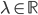
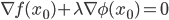
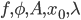
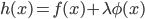
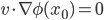
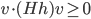
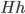
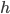
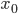
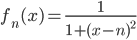
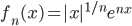
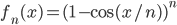
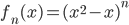
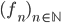
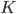
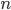
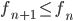
![[a,b]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_2c3d331bc98b44e71cb2aae9edadca7e.gif)
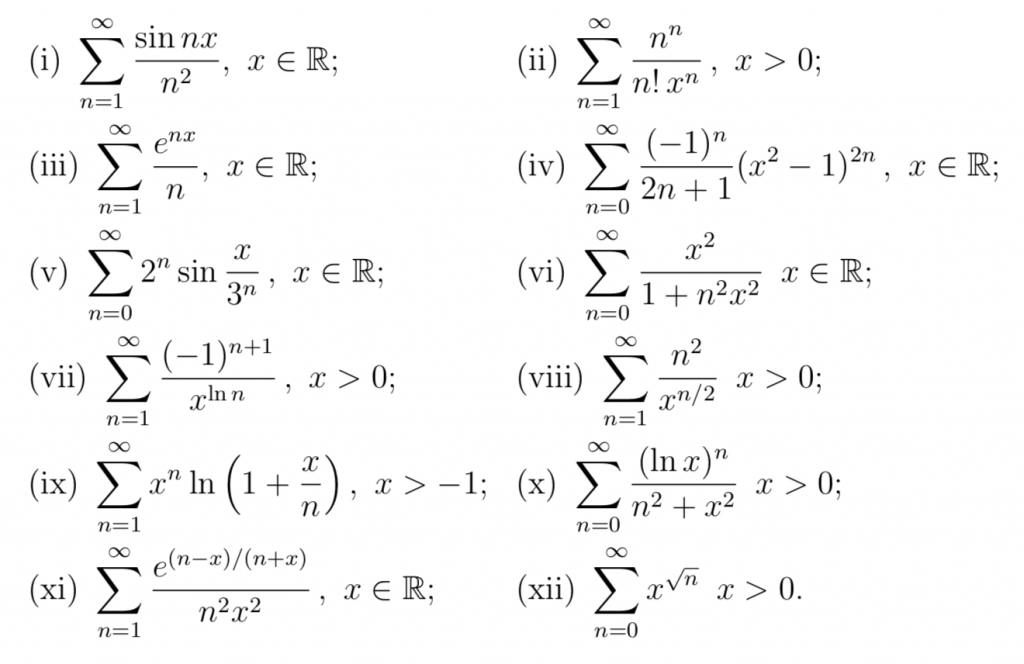
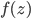
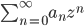
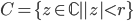
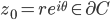
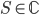
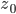
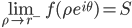
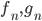
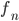
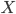
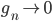
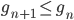
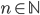
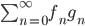
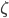
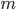
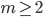
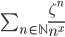
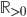
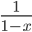
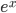
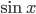

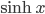
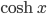
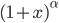
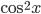
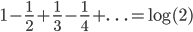
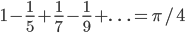
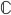
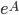
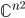
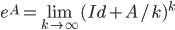
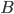
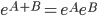
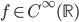
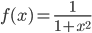
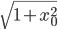
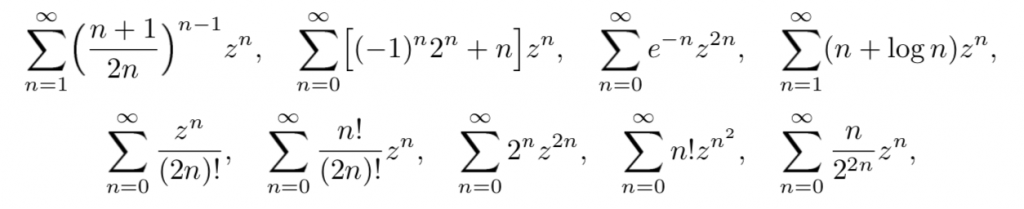
![\omega:[0,\infty)\to [0,\infty]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_cb04b119908c9364085edf9445165beb.gif)
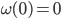
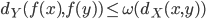
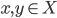
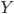
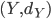
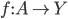
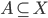
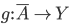
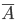
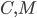
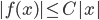
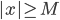
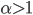
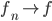


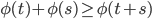
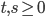
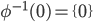
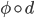
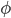
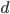
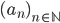
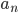
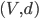
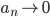
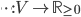
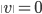
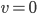
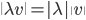
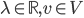
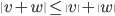
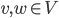

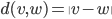
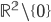
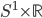
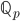
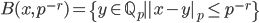
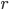
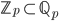
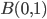
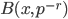
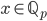
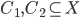
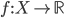
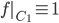
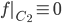
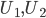
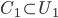
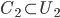
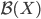
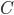
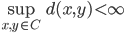
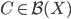
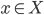
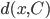
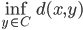
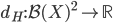
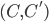
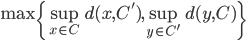
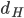
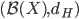
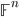
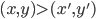
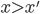

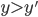
![[0,1]\times [0,1]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_38c7b34812cb087f3562f9ebc984e3c8.gif)
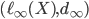
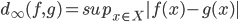
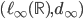
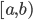
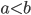

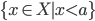
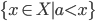
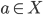
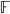
![\mathbb{F}[x_1,\ldots,x_n]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_46c92821ebc8730ff21045240c369124.gif)
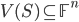
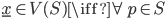
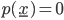
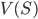
![S\subseteq\mathbb{F}[x_1,\ldots,x_n]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_710ac9045199bb71a2a4c98b52bd8216.gif)
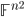
![\mathbb{R}, [0,1], [0,1), (0,1), S^1, S^2, \mathbb{R}^2](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_3132a02eefb9fb3fcfd0a6d00c3a9117.gif)
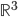
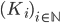

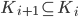

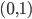
![[0,1]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_ccfcd347d0bf65dc77afe01a3306a96b.gif)
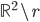
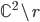
![\{(x,\sin(1/x)\mid x\in (0,1]\}](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_80bd5fd982aa79b9158b5634ae9df56d.gif)
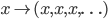
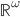
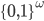
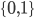
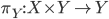





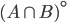

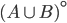
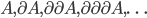
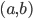
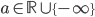
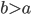
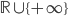
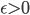
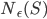
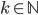
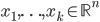
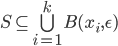
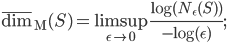
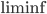
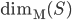
![S=[0,1]^d\times \{0\}^{n-d}](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_a988b33b3042128d545525007712dbe6.gif)
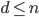
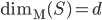
![(S=[0,1]\cap\mathbb{Q})\times \{0\}^{n-1}](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_d9d29590cba9ddc8a3dda077d4544bd9.gif)
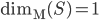
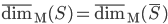
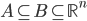
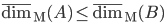
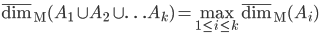
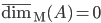

![N^{box}_\epsilon(S)=\min\{k\mid \exists x_1,\ldots, x_k\in\mathbb{R}^n : S\subseteq \bigcup_{i=1}^k x_i+[-\epsilon/2,\epsilon/2]^n\}](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_52631e50e19e14ed164699ccec509e64.gif)
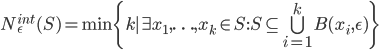
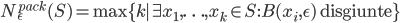
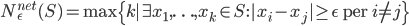
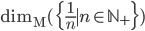
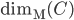
![C\subset [0,1]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_9d9b63f05877e2fd091ca6df4f6eb2a1.gif)
![\operatorname{dim_M}(\{(x,\sin(1/x))\mid x\in (0,1]\})](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_c574b22a4525b42a7b6f267ea15f9120.gif)
![\{(x,f(x))\mid x\in[0,1]\}\subset \mathbb{R}^2](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_6b62670e3075da92e5d5da27ab38b49c.gif)