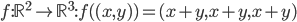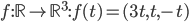Applications linéaires, noyau, image
QUESTIONS :
[♠︎❄︎❄︎☕︎] Dire si les fonctions suivantes sont linéaires ou pas, et justifier sa réponse
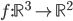 :
: 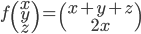
![f:\mathbb{R}[x]\to\mathbb{R}](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_851901561ae8a833b2329cd39ccd30d8.gif) :
: 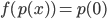
![f:\mathbb{R}[x]\to\mathbb{R}](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_851901561ae8a833b2329cd39ccd30d8.gif) :
: 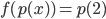
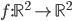 :
: 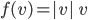
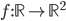 :
: 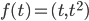
![f:\mathbb{R}[x]\to\mathbb{R}[x]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_145dc1ddf87117f11d547f8b90f72a21.gif) :
: 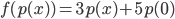
- (*)
![f:\mathbb{R}[x]\to\mathbb{R}[x]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_145dc1ddf87117f11d547f8b90f72a21.gif) :
: 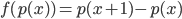
[♠︎❄︎❄︎] Dire s'il existe une application linéaire  de
de  dans
dans 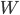 telle que
telle que 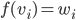 dans les cas suivants ; quand une telle
dans les cas suivants ; quand une telle  existe, préciser si elle est unique :
existe, préciser si elle est unique :
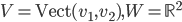
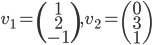 ,
, 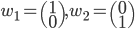
[♠︎❄︎❄︎☕︎] Pour chacune des applications linéaires suivantes, déterminer la dimension du noyau et la dimension de l'image :



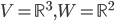

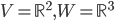

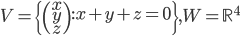
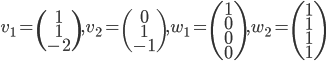
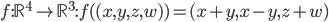
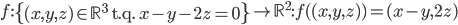
![f:\{ax^3+bx^2+cx+d\mbox{ t.q. }a,b,c,d\in\mathbb{R}\}\to\mathbb{R}[x] : f(p(x))=p'(x)](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_857f266940d4571f253f99e320ff7927.gif)