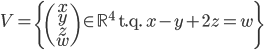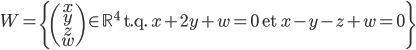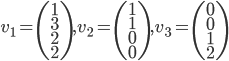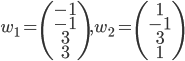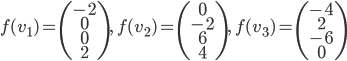Problème 1. Soient
et
les espaces vectoriels suivants :
- Quelle est la dimension de
?
L'espace  est défini comme sous-espace de
est défini comme sous-espace de 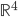 par une seule équation, donc sa dimension est
par une seule équation, donc sa dimension est 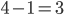 .
.
- Exprimer
comme le noyau d'une application linéaire entre
et $\mathbb{R}^2$. En déduire la dimension de
.
L'espace 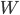 est le noyau de l'application linéaire
est le noyau de l'application linéaire 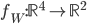 représentée (par rapport aux bases canoniques de
représentée (par rapport aux bases canoniques de 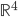 et
et  ) par la matrice
) par la matrice
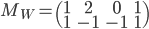 .
.
On a 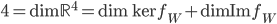 ; l'image de
; l'image de 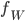 , qui est engendrée par les colonnes de la matrice
, qui est engendrée par les colonnes de la matrice 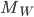 , est incluse dans
, est incluse dans  et contient deux vecteurs non-colinéaires (par exemple les deux premières colonnes de la matrice
et contient deux vecteurs non-colinéaires (par exemple les deux premières colonnes de la matrice 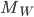 ) donc a dimension 2.
) donc a dimension 2.
Finalement, 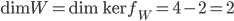 .
.
On considère les familles de vecteurs suivantes :
- Montrer que
est une base de
, et que
est une base de
.
Les vecteurs 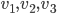 sont trois vecteurs libres (
sont trois vecteurs libres (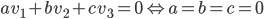 ) de
) de  (car leur coordonnées satisfont à l'équation
(car leur coordonnées satisfont à l'équation 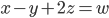 ). La dimension de
). La dimension de  est trois, donc
est trois, donc 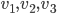 est une base de
est une base de  .
.
De même pour 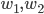 . Je ne vais pas écrire plus de détails, parce que essentiellement tout le monde a réussi cette question. Bravo !
. Je ne vais pas écrire plus de détails, parce que essentiellement tout le monde a réussi cette question. Bravo !
- Existe-t-il une application linéaire de
vers
dont le noyau est
?
Non ! Une application linéaire  de
de  vers
vers 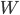 est toujours telle que
est toujours telle que 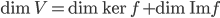 . Par contre, on sait que
. Par contre, on sait que 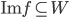 , donc
, donc 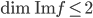 , dont on obtient
, dont on obtient 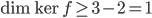 ; la dimension du noyau de
; la dimension du noyau de  est au moins 1, donc le noyau ne peut dans aucun cas être
est au moins 1, donc le noyau ne peut dans aucun cas être 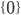 .
.
- Montrer qu'il existe une unique application linéaire
telle que
Existence et unicité sont une conséquence du fait que 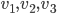 forment une base de
forment une base de  , et que les vecteurs
, et que les vecteurs 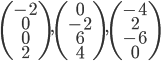 appartiennent à
appartiennent à 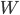 .
.
- Quelle est la matrice associée à
par rapport aux bases
et
?
Les colonnes de 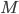 contiennent les coordonnées des vecteurs
contiennent les coordonnées des vecteurs 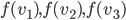 par rapport à la base
par rapport à la base 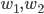 . En faisant les calculs, on obtient
. En faisant les calculs, on obtient
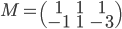 .
.
- Calculer
(exprimer le résultat comme un vecteur de
).
On a 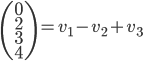 , donc
, donc  .
.
On pourrait aussi calculer 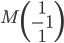 (où
(où 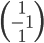 est le vecteur des coordonnées de
est le vecteur des coordonnées de 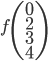 par rapport à la base
par rapport à la base 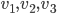 ), ce qui nous donne le vecteur
), ce qui nous donne le vecteur 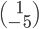 . On a donc
. On a donc 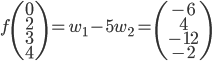 .
.
- Quelle est la dimension de
? En déduire la dimension de
.
On sait que 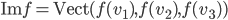 ; on sait aussi que
; on sait aussi que 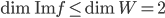 . Comme les vecteurs
. Comme les vecteurs 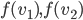 ne sont pas colinéaires, on déduit que
ne sont pas colinéaires, on déduit que 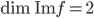 .
.
Par conséquence, on a 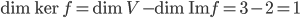 .
.
- Déterminer une base de
(on exprimera les éléments de cette base comme vecteurs de
).
On a que 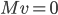 pour un vecteur
pour un vecteur 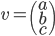 si et seulement si
si et seulement si 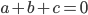 et
et 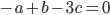 , c'est-à-dire pour les vecteurs
, c'est-à-dire pour les vecteurs 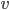 de la forme
de la forme 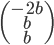 .
.
Les vecteurs du noyau de  sont donc ceux qui s'écrivent sous la forme
sont donc ceux qui s'écrivent sous la forme 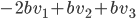 ; en posant
; en posant 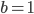 on trouve que le vecteur
on trouve que le vecteur 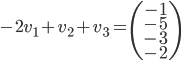 forme une base de
forme une base de 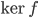 .
.