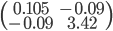Une entreprise fabrique des pièces d’usines. Parmi les pièces fabriquées, 90 % satisfont aux normes de qualité, 5 % ne satisont pas à ces normes mais fonctionnent quand même et 5 % sont défectueuses. Pour essayer de connaître la fiabilité du fabricant, un client potentiel choisit au hasard 2 pièces. On appelle
le nombre de pièces défectueuses et
le nombre de pièces aux normes.
1. Calculer la loi du coupleet sa matrice de variance-covariance.
2. Trouver les lois deet de
, puis leurs espérances.
3. Retrouver ce dernier résultat en utilisant le principe de linéarité de l’espérance.
4.et
sont-elles indépendantes ?
Il est important de bien comprendre la situation decrite dans l'exo : les pièces fabriquées tombent chacune dans une de trois catégories :
- pièces aux normes (
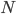 )
) - pièces fonctionnantes, mais pas aux normes (
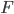 )
) - pièces défectueuses (bien sûr, pas aux normes) (
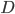 )
)
Les trois ensambles 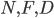 forment une partition de l'ensamble de pièces, au sens où il n'y a pas d'intersection entre chaque couple d'ensembles (il ne peut pas y avoir, par exemple, une pièce defectueuse mais aux normes, ou une pièce qui est dans
forment une partition de l'ensamble de pièces, au sens où il n'y a pas d'intersection entre chaque couple d'ensembles (il ne peut pas y avoir, par exemple, une pièce defectueuse mais aux normes, ou une pièce qui est dans 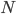 et
et 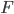 en même temps).
en même temps).
On prend deux pièces au hazard ; on va les appeler 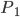 et
et 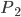 . Pour chaque pièce (de manière indépendante) on a
. Pour chaque pièce (de manière indépendante) on a 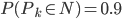 et
et 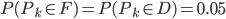 . On se demande combien de pièces sont défectueuses (
. On se demande combien de pièces sont défectueuses ( ) et combien sont aux normes (
) et combien sont aux normes ( ) parmi les deux pièces choisies, et on cherche à déterminer la loi du couple
) parmi les deux pièces choisies, et on cherche à déterminer la loi du couple 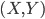 .
.
Les valeurs possibles pour  sont
sont 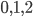 : soit les deux pièces sont défectueuse, soit il y a une qui est défectueuse et une qui marche, soit les deux pièces sont fonctionnantes. De même, les valeurs possibles pour
: soit les deux pièces sont défectueuse, soit il y a une qui est défectueuse et une qui marche, soit les deux pièces sont fonctionnantes. De même, les valeurs possibles pour  sont
sont 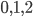 .
.
Il faut donc calculer 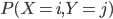 pour
pour 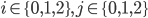 (c'est à dire qu'il y a 9 valeurs à calculer) ; on va considérer chaque cas :
(c'est à dire qu'il y a 9 valeurs à calculer) ; on va considérer chaque cas :
- il est immédiat de voir que
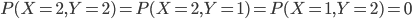 , car ces situations sont impossibles : on n'a que deux pièce, et on sait que si une pièce est défectueuse alors elle n'est pas aux normes et inversement ;
, car ces situations sont impossibles : on n'a que deux pièce, et on sait que si une pièce est défectueuse alors elle n'est pas aux normes et inversement ; 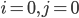 : cela correspond à
: cela correspond à 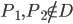 et
et 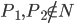 , donc
, donc 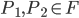 ; comme
; comme 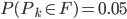 ,
, 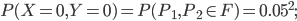
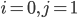 : on a une pièce aux normes ; comme aucune pièce n'est défectueuse, l'autre pièce doit être dans
: on a une pièce aux normes ; comme aucune pièce n'est défectueuse, l'autre pièce doit être dans 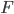 (elle n'est pas défectueuse ni aux normes) ; on a donc
(elle n'est pas défectueuse ni aux normes) ; on a donc 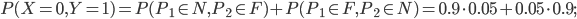
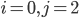 : les deux pièce sont aux normes, ce qui arrive avec proba
: les deux pièce sont aux normes, ce qui arrive avec proba 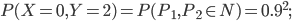
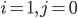 : une pièce défectueuse, l'autre pas aux normes (mais fonctionnante) ;
: une pièce défectueuse, l'autre pas aux normes (mais fonctionnante) ; 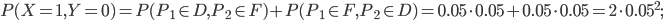
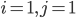 : une pièce défectueuse, l'autre aux normes ;
: une pièce défectueuse, l'autre aux normes ; 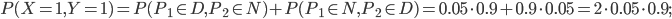
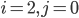 : les deux pièces sont défectueuses ;
: les deux pièces sont défectueuses ; 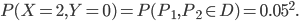
On trouve donc le tableau suivant pour la loi du couple :
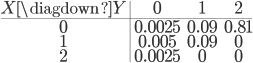
dont les lois marginales et espérances
\begin{array}{c|ccc|c} X & 0 & 1 & 2 & E(X) \\\hline & 0.9025 & 0.095 & 0.0025 & 0.1\end{array}\begin{array}{c|ccc|c} Y & 0 & 1 & 2 & E(Y) \\\hline & 0.01 & 0.18 & 0.81 & 1.8\end{array}
On nous demande aussi de retrouver les espérances en utilisant la linéarité ; ça serait plus simple à faire si on savait ce que c'est que 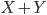 , mais tout ce qu'on sait est que
, mais tout ce qu'on sait est que 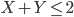 . Par ailleurs, si on appelle
. Par ailleurs, si on appelle 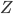 le nombre de pièces fonctionnantes mais pas aux normes parmi les deux, on sait que
le nombre de pièces fonctionnantes mais pas aux normes parmi les deux, on sait que 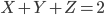 (le nombre totale de pièces) et on sait aussi que, comme la proba qu'une pièce soit dans
(le nombre totale de pièces) et on sait aussi que, comme la proba qu'une pièce soit dans 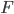 est la même que celle d'être dans
est la même que celle d'être dans 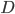 , la loi de
, la loi de 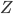 est la même que la loi de
est la même que la loi de  . On a alors
. On a alors 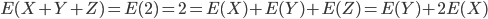 , d'où
, d'où 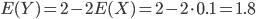 , ce qui est bien ce qu'on avait trouvé avec le calcul direct de
, ce qui est bien ce qu'on avait trouvé avec le calcul direct de 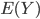 .
.
Finalement,  et
et  ne sont pas indépendants ; cela est bien évident (par exemple, si
ne sont pas indépendants ; cela est bien évident (par exemple, si 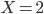 alors il est impossible d'avoir
alors il est impossible d'avoir 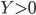 : plus
: plus  est grand, plus
est grand, plus  doit être petit), mais on va calculer la matrice variance-covarance, comme on nous demande de faire dans la première question. On a :
doit être petit), mais on va calculer la matrice variance-covarance, comme on nous demande de faire dans la première question. On a :
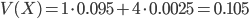
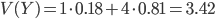
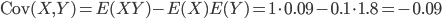
La covariance est non nulle, donc  et
et  ne sont pas indépendants. La matrice variance-covariance est la suivante :
ne sont pas indépendants. La matrice variance-covariance est la suivante :