Breve nota: anziché segnare alcuni esercizi come "più difficili" o extra, ho deciso di indicare con ☞ un sottoinsieme degli esercizi "minimale" che consiglio a tutti di assicurarsi di essere capaci di svolgere e – cosa non scontata – scrivere bene. Nessuno dei problemi ☞ dovrebbe porre difficoltà insormontabili (a meno di typo o errori in qualche esercizio, che sono ovviamente possibili e che vi prego di far presenti a esercitazione!). Buon weekend e buon lavoro!
Alcuni esempi di spazi topologici
☞ 16. [Svolto 16/2] (Retta di Sorgenfrey) Su  , si consideri la topologia generata dagli intervalli della forma
, si consideri la topologia generata dagli intervalli della forma 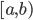 con
con 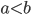 . Mostrare che è una topologia strettamente più fine di quella standard (gli aperti "normali" sono tutti aperti in questa topologia, ma non viceversa). Quali sottoinsiemi in questa topologia sono connessi? Cosa riuscite a dire sui sottoinsiemi compatti in questa topologia?
. Mostrare che è una topologia strettamente più fine di quella standard (gli aperti "normali" sono tutti aperti in questa topologia, ma non viceversa). Quali sottoinsiemi in questa topologia sono connessi? Cosa riuscite a dire sui sottoinsiemi compatti in questa topologia?
☞ 17. [Svolto 16/2] (Topologia d'ordine) Dato un insieme  dotato di un ordine totale
dotato di un ordine totale  , la topologia d'ordine su
, la topologia d'ordine su  è quella generata dagli insiemi della forma
è quella generata dagli insiemi della forma 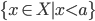 e
e 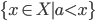 , dove
, dove 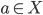 . Ad esempio, la topologia di
. Ad esempio, la topologia di  è la sua topologia d'ordine per l'ordinamento standard. Mostrare un esempio di sottoinsieme di
è la sua topologia d'ordine per l'ordinamento standard. Mostrare un esempio di sottoinsieme di  la cui topologia indotta non sia quella d'ordine.
la cui topologia indotta non sia quella d'ordine.
18. [Svolto 16/2] (Topologia di Zariski) Sia 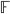 un campo. Dato un insieme
un campo. Dato un insieme 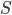 di polinomi in
di polinomi in ![\mathbb{F}[x_1,\ldots,x_n]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_46c92821ebc8730ff21045240c369124.gif) , chiamiamo
, chiamiamo 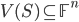 l'insieme degli zeri comuni a tutti gli elementi di
l'insieme degli zeri comuni a tutti gli elementi di 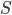 (
(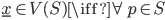
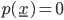 ). Dimostrare che la collezione di sottoinsiemi di
). Dimostrare che la collezione di sottoinsiemi di 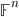 che sono della forma
che sono della forma 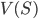 per un qualche
per un qualche ![S\subseteq\mathbb{F}[x_1,\ldots,x_n]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_710ac9045199bb71a2a4c98b52bd8216.gif) è l'insieme dei chiusi di una topologia su
è l'insieme dei chiusi di una topologia su 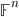 , detta topologia di Zariski. Mostrare che lo spazio
, detta topologia di Zariski. Mostrare che lo spazio 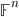 dotato di tale topologia non è T2 (cioè Hausdorff) a meno che
dotato di tale topologia non è T2 (cioè Hausdorff) a meno che 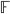 non sia finito (nel qual caso, in cosa consiste la topologia di Zariski?) Dimostrare che, se
non sia finito (nel qual caso, in cosa consiste la topologia di Zariski?) Dimostrare che, se 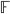 è infinito, interpretando
è infinito, interpretando 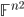 come l'insieme delle matrici
come l'insieme delle matrici 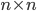 a coefficienti in
a coefficienti in 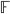 , le matrici invertibili sono dense in
, le matrici invertibili sono dense in 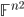 per la topologia di Zariski. Utilizzare questo fatto per dimostrare il Teorema di Binet.
per la topologia di Zariski. Utilizzare questo fatto per dimostrare il Teorema di Binet.
☞ 19. [Svolto 16/2] Per tutte le possibili coppie di spazi della lista seguente, esibire un omeomorfismo fra i due o dimostrare che i due spazi non sono omeomorfi: ![\mathbb{R}, [0,1], [0,1), (0,1), S^1, S^2, \mathbb{R}^2](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_3132a02eefb9fb3fcfd0a6d00c3a9117.gif) .
.
20. Dimostrare che  ed
ed 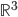 non sono omeomorfi (pensateci, ma questo è più difficile di quanto non sembri e certamente facoltativo)!
non sono omeomorfi (pensateci, ma questo è più difficile di quanto non sembri e certamente facoltativo)!
Compattezza, connessione
☞ 21. [Svolto 16/2] Dimostrare che un compatto in uno spazio T2 è chiuso e fornire un esempio di un compatto non chiuso. Dimostrare che una funzione continua e bigettiva da uno spazio compatto a uno spazio T2 è un omeomorfismo. L'affermazione rimane vera rilassando l'ipotesi "compatto" o l'ipotesi "T2"?
☞ 22. [Svolto 16/2] Dimostrare che, data una successione di compatti chiusi non vuoti "annidati" 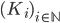 in uno spazio topologico
in uno spazio topologico  tale che per
tale che per 
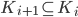 , l'intersezione
, l'intersezione  è non vuota. Si può eliminare la condizione "compatti"? Si può eliminare la condizione "chiusi"? (Questo è un lemma IMPORTANTE che forse avrete visto o vedrete a lezione: siate capaci di dimostrarlo e tenetelo presente come strumento da usare!)
è non vuota. Si può eliminare la condizione "compatti"? Si può eliminare la condizione "chiusi"? (Questo è un lemma IMPORTANTE che forse avrete visto o vedrete a lezione: siate capaci di dimostrarlo e tenetelo presente come strumento da usare!)
☞ 23. [Svolto 16/2] Esiste una funzione continua bigettiva da 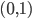 in
in ![[0,1]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_ccfcd347d0bf65dc77afe01a3306a96b.gif) ?
?
☞ 24. L'insieme 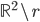 , dove
, dove 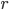 è una retta, è connesso? L'insieme
è una retta, è connesso? L'insieme 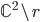 , dove
, dove 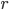 è un sottospazio affine di dimensione (su
è un sottospazio affine di dimensione (su 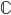 ) 1, è connesso?
) 1, è connesso?
25. Dimostrare che la chiusura dell'insieme ![\{(x,\sin(1/x)\mid x\in (0,1]\}](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_80bd5fd982aa79b9158b5634ae9df56d.gif) è connessa, ma non connessa per archi.
è connessa, ma non connessa per archi.
Topologia prodotto
☞ 26. Dimostrare che le proiezioni per la topologia prodotto sono continue e aperte. Dimostrare che una funzione da uno spazio topologico a un prodotto di spazi topologici è continua se e solo se lo sono le sue composizioni con le proiezioni canoniche.
☞ 27. Dimostrare che prodotto di T2 è T2 e che prodotto di connessi è connesso. Dimostrare che il prodotto di due spazi compatti è compatto.
28. Dimostrare che, con la box topology generata da tutti i rettangoli (e non dai soli insiemi cilindrici) il prodotto di spazi topologici compatti non è necessariamente compatto. Dimostrare che la funzione 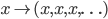 da
da  in
in 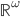 è continua se su
è continua se su 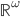 si considera la topologia prodotto, ma non se su
si considera la topologia prodotto, ma non se su 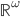 si considera la box topology.
si considera la box topology.
29. Dimostrare che lo spazio 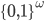 con la topologia prodotto (di una quantità numerabile di copie della topologia discreta su
con la topologia prodotto (di una quantità numerabile di copie della topologia discreta su 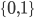 ) è omeomorfo all'insieme di Cantor con la topologia indotta dalla topologia di
) è omeomorfo all'insieme di Cantor con la topologia indotta dalla topologia di  .
.
30. [Parzialmente svolto 16/2] Ecco una caratterizzazione alternativa forse un po' sorprendente della compattezza. Dimostrare che uno spazio topologico  è compatto se e solo se per ogni spazio topologico
è compatto se e solo se per ogni spazio topologico  la proiezione
la proiezione 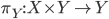 è chiusa.
è chiusa.


