Spazi metrici e topologie indotte
☞ 31. Dato uno spazio metrico 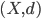 , sia
, sia  una funzione debolmente crescente e subadditiva, cioè tale che si abbia
una funzione debolmente crescente e subadditiva, cioè tale che si abbia 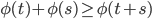 per
per 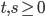 , tale che
, tale che 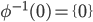 . Mostrare che
. Mostrare che 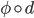 è ancora una distanza su
è ancora una distanza su  . Mostrare che se
. Mostrare che se 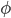 è continua in 0 allora la topologia generata da
è continua in 0 allora la topologia generata da 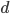 è la stessa della topologia generata da
è la stessa della topologia generata da 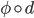 . Il viceversa è vero?
. Il viceversa è vero?
☞ 32. Sia 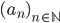 una successione di elementi di uno spazio vettoriale
una successione di elementi di uno spazio vettoriale  dotato di una distanza ultrametrica (vedi definizione nelle note)
dotato di una distanza ultrametrica (vedi definizione nelle note) 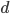 che sia invariante per traslazioni e lo renda completo; si dimostri che la serie (i.e. la successione delle somme parziali) degli
che sia invariante per traslazioni e lo renda completo; si dimostri che la serie (i.e. la successione delle somme parziali) degli 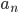 converge in
converge in 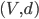 se e solo se
se e solo se 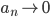 in
in 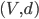 .
.
33. Sia  uno spazio vettoriale su
uno spazio vettoriale su  . Una norma su
. Una norma su  è una funzione
è una funzione 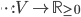 tale che valgano:
tale che valgano:  se e solo se
se e solo se 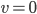 ;
; 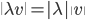 per ogni
per ogni 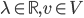 ;
; 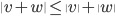 per ogni
per ogni 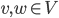 .
.
Dimostrare che, se  è una norma, allora
è una norma, allora 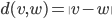 è una distanza su
è una distanza su  . Dimostrare che, date due norme su uno spazio
. Dimostrare che, date due norme su uno spazio  di dimensione finita, le loro distanze corrispondenti sono bi-Lipschitz equivalenti. La conclusione vale anche per
di dimensione finita, le loro distanze corrispondenti sono bi-Lipschitz equivalenti. La conclusione vale anche per  di dimensione infinita?
di dimensione infinita?
☞ 34. Mostrare che 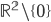 (con la metrica euclidea) e
(con la metrica euclidea) e 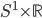 (con la metrica prodotto fra la metrica geodetica e quella euclidea) sono omeomorfi (per le rispettive topologie indotte) ma non isometrici.
(con la metrica prodotto fra la metrica geodetica e quella euclidea) sono omeomorfi (per le rispettive topologie indotte) ma non isometrici.
35. Fornire, se esiste, un esempio di uno spazio topologico compatto ma non sequenzialmente compatto e un esempio di spazio topologico sequenzialmente compatto ma non compatto.
36. Sia 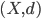 uno spazio metrico tale che ogni funzione continua da
uno spazio metrico tale che ogni funzione continua da  in
in  abbia massimo. Dimostrare che
abbia massimo. Dimostrare che  è compatto.
è compatto.
Razionali e interi 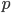 -adici
-adici
☞ 37. Su 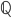 , si consideri la distanza
, si consideri la distanza 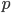 -adica descritta dalle note del corso. Si dimostri che è una ultrametrica (vedi note) e che
-adica descritta dalle note del corso. Si dimostri che è una ultrametrica (vedi note) e che 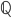 non è completo per questa distanza. Sia
non è completo per questa distanza. Sia 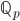 un completamento del suddetto spazio metrico; dimostrare che le palle chiuse in
un completamento del suddetto spazio metrico; dimostrare che le palle chiuse in 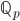 (i.e. gli insiemi della forma
(i.e. gli insiemi della forma 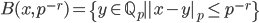 , con
, con 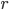 intero positivo) sono sia chiuse che aperte. Dimostrare che
intero positivo) sono sia chiuse che aperte. Dimostrare che 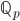 (con la topologia indotta dalla distanza
(con la topologia indotta dalla distanza 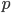 -adica) è totalmente disconnesso e T2.
-adica) è totalmente disconnesso e T2.
38. Si dimostri che lo spazio metrico 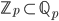 degli interi
degli interi 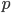 -adici, dato dalla palla
-adici, dato dalla palla 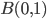 nella notazione dell'esercizio precedente, è compatto e omeomorfo a
nella notazione dell'esercizio precedente, è compatto e omeomorfo a 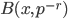 per qualunque intero
per qualunque intero 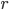 e
e 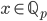 .
.
La distanza di Hausdorff
☞ 39. Sia 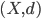 uno spazio metrico e siano
uno spazio metrico e siano 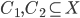 due chiusi disgiunti. Dimostrare che esiste una funzione continua
due chiusi disgiunti. Dimostrare che esiste una funzione continua 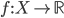 tale che
tale che 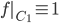 e
e 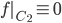 . Dedurre che esistono due aperti disgiunti
. Dedurre che esistono due aperti disgiunti 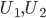 tali che
tali che 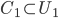 ,
, 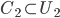 .
.
40. La tesi dell'esercizio 39 è vera per ogni spazio topologico T2?
41. Sia 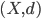 uno spazio metrico. Sia
uno spazio metrico. Sia 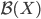 l'insieme dei chiusi limitati di
l'insieme dei chiusi limitati di  (cioè dei chiusi
(cioè dei chiusi 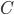 tali che
tali che 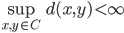 ). Dato
). Dato 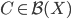 e
e 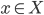 , scriviamo
, scriviamo 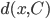 per
per 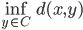 . Si consideri la funzione
. Si consideri la funzione 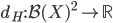 che manda
che manda 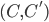 in
in 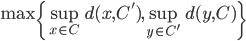 . Dimostrare che
. Dimostrare che 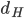 è una distanza su
è una distanza su 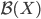 .
.
42. Dimostrare che, se 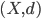 è compatto, allora
è compatto, allora 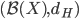 è compatto. Se lo spazio
è compatto. Se lo spazio  è completo, è vero che
è completo, è vero che 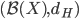 è completo?
è completo?
43. Mostrare che le approssimazioni standard della stella di Koch convergono formalmente verso la stella di Koch secondo la distanza 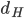 , e similmente per i soliti chiusi la cui intersezione dà il Cantor.
, e similmente per i soliti chiusi la cui intersezione dà il Cantor.
Metrizzabilità e isometrie
44. Uno spazio topologico è metrizzabile se esiste una metrica sullo spazio che induca la sua topologia. Determinare, per i seguenti spazi, se sono o meno metrizzabili (se sì, esibire una metrica appropriata): qualunque spazio con la topologia discreta; la retta di Sorgenfrey; la topologia di Zariski su 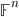 infinito; la topologia d'ordine su
infinito; la topologia d'ordine su  data dall'ordine "
data dall'ordine "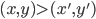 se e solo se
se e solo se 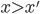 o
o  e
e 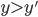 "; la topologia d'ordine data dall'ordine sopra descritto su
"; la topologia d'ordine data dall'ordine sopra descritto su ![[0,1]\times [0,1]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_38c7b34812cb087f3562f9ebc984e3c8.gif) .
.
45. Dato uno spazio metrico 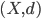 , sia
, sia 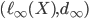 lo spazio metrico delle funzioni da
lo spazio metrico delle funzioni da  a
a  con la distanza del sup (
con la distanza del sup (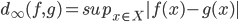 ). Dimostrare che, qualunque sia
). Dimostrare che, qualunque sia  ,
, 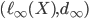 è completo.
è completo.
46. Dimostrare che qualunque spazio metrico 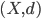 è isometrico a un sottoinsieme di
è isometrico a un sottoinsieme di 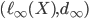 (consiglio: provate a dimostrarlo prima nel caso in cui
(consiglio: provate a dimostrarlo prima nel caso in cui  sia limitato). Dedurre che ogni spazio metrico la cui cardinalità non sia più che quella di
sia limitato). Dedurre che ogni spazio metrico la cui cardinalità non sia più che quella di  si può immergere isometricamente in
si può immergere isometricamente in 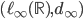 .
.


