Come promesso, un set di esercizi un po' più tardivo e un po' più scarno per questa volta!
Sia 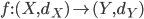 una funzione. Un modulo di continuità per
una funzione. Un modulo di continuità per  è una funzione
è una funzione ![\omega:[0,\infty)\to [0,\infty]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_cb04b119908c9364085edf9445165beb.gif) debolmente crescente e continua in
debolmente crescente e continua in 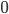 tale che si abbia
tale che si abbia 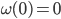 ,
, 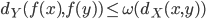 per
per 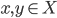 .
.
47. Dimostrare che  ha un modulo di continuità se e solo se è uniformemente continua.
ha un modulo di continuità se e solo se è uniformemente continua.
48. Dimostrare inoltre che, se  ha un modulo di continuità, ne ha uno che sia continuo dove non è infinito.
ha un modulo di continuità, ne ha uno che sia continuo dove non è infinito.
49. Dimostrare che, se  è un intervallo e
è un intervallo e  è
è  con la distanza euclidea,
con la distanza euclidea,  è uniformemente continua se e solo se ammette modulo di continuità finito. Cosa si può dire in generale sull'esistenza o meno di un modulo di continuità finito?
è uniformemente continua se e solo se ammette modulo di continuità finito. Cosa si può dire in generale sull'esistenza o meno di un modulo di continuità finito?
50. Supponiamo che 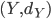 sia completo e consideriamo
sia completo e consideriamo 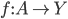 , dove
, dove 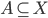 . Mostrare che, se
. Mostrare che, se  è uniformemente continua, allora si estende in modo unico a una funzione
è uniformemente continua, allora si estende in modo unico a una funzione 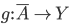 continua, che è anche uniformemente continua. Se
continua, che è anche uniformemente continua. Se 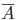 è compatto si può in effetti caratterizzare così la continuità uniforme:
è compatto si può in effetti caratterizzare così la continuità uniforme:  è uniformemente continua se e solo se si estende a
è uniformemente continua se e solo se si estende a 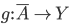 continua.
continua.
51. Mostrare (idealmente utilizzando il modulo di continuità!) che se 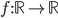 è uniformemente continua, allora esistono costanti positive
è uniformemente continua, allora esistono costanti positive 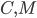 tali che
tali che 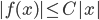 per
per 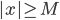 .
.
52. Dimostrare che se 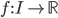 (con
(con 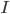 intervallo) è
intervallo) è  -Hölderiana con
-Hölderiana con 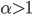 allora è costante.
allora è costante.
53. Costruire (se esiste) un esempio di funzione in ciascuna categoria: ![f:[0,1]\to\mathbb{R}](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_2f88c23f13b9b1904c39f298cd688669.gif) uniformemente continua ma non Hölderiana;
uniformemente continua ma non Hölderiana;  continua ma non uniformemente continua;
continua ma non uniformemente continua;  uniformemente continua fra spazi metrici che non sia limitata su ogni limitato;
uniformemente continua fra spazi metrici che non sia limitata su ogni limitato; 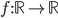 continua e non monotona su nessun intervallo.
continua e non monotona su nessun intervallo.
54. Dimostrare che esiste una topologia sull'insieme delle funzioni da  a
a  tale che
tale che 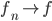 secondo questa topologia se e solo se le
secondo questa topologia se e solo se le 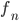 convergono a
convergono a  puntualmente, ma che non esiste una metrica che induca questa topologia.
puntualmente, ma che non esiste una metrica che induca questa topologia.
55. È vero che, se 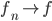 funzioni da
funzioni da  in
in  convergono uniformemente e le
convergono uniformemente e le 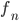 sono uniformemente continue, allora il limite
sono uniformemente continue, allora il limite  è uniformemente continuo? È vero se, anziché la convergenza uniforme su
è uniformemente continuo? È vero se, anziché la convergenza uniforme su  , vale la convergenza uniforme su tutti i compatti
, vale la convergenza uniforme su tutti i compatti  ?
?


