Perdonate la lista degli esercizi arrivata tardissimo: avete però un sacco di tempo per pensarci, perché come dicevamo l'altra volta correggeremo esercizi vecchi questo giovedì (chi non ha risposto al questionario potrebbe a questo punto farlo, se possibile entro domani, anche solo segnalando i problemi che vuole vedere corretti se ne ha!). Notate che nella seconda parte di questa mandata ci sono (anche) esercizi sugli argomenti che tratterete oggi a lezione. Vi pubblicherò con calma un'ulteriore mandata di esercizi di calcolo differenziale quando l'avrete fatto, e poi ne correggeremo un po' insieme dopo i colloqui.
Convergenza uniforme
☞ 56. Per le seguenti successioni di funzioni da  in
in  , si determini l'insieme dei punti sui quali convergono e se su tale insieme convergono o meno uniformemente:
, si determini l'insieme dei punti sui quali convergono e se su tale insieme convergono o meno uniformemente:
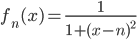 ;
;
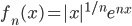 ;
;
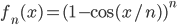 ;
;
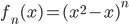 .
.
☞ (importante ma non banale) 57. [Svolto il 28/3] Sia 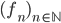 una successione di funzioni reali continue su un compatto
una successione di funzioni reali continue su un compatto 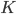 di
di  , decrescente nel senso che per ogni
, decrescente nel senso che per ogni 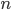 si abbia
si abbia 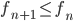 su
su 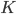 , che converga puntualmente a una funzione continua
, che converga puntualmente a una funzione continua  su
su 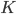 . Dimostrare che la convergenza è in realtà uniforme. Questo risultato sarebbe vero se non fossimo su un compatto? Se il limite non fosse continuo? Se non si avesse definitivamente
. Dimostrare che la convergenza è in realtà uniforme. Questo risultato sarebbe vero se non fossimo su un compatto? Se il limite non fosse continuo? Se non si avesse definitivamente 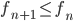 ?
?
☞ 58. [Svolto il 28/3] Sia 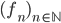 una successione di funzioni reali continue definite su un intervallo chiuso
una successione di funzioni reali continue definite su un intervallo chiuso ![[a,b]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_2c3d331bc98b44e71cb2aae9edadca7e.gif) , ciascuna debolmente crescente, che convergano puntualmente verso una funzione
, ciascuna debolmente crescente, che convergano puntualmente verso una funzione  continua su
continua su ![[a,b]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_2c3d331bc98b44e71cb2aae9edadca7e.gif) . Si dimostri che la convergenza è uniforme.
. Si dimostri che la convergenza è uniforme.
59. Dimostrare che l'indicatrice dei razionali non è limite puntuale di funzioni continue.
Serie di funzioni
☞ (almeno alcune!) 60. Discutere la convergenza (puntuale/assoluta/uniforme/totale) delle seguenti serie di funzioni
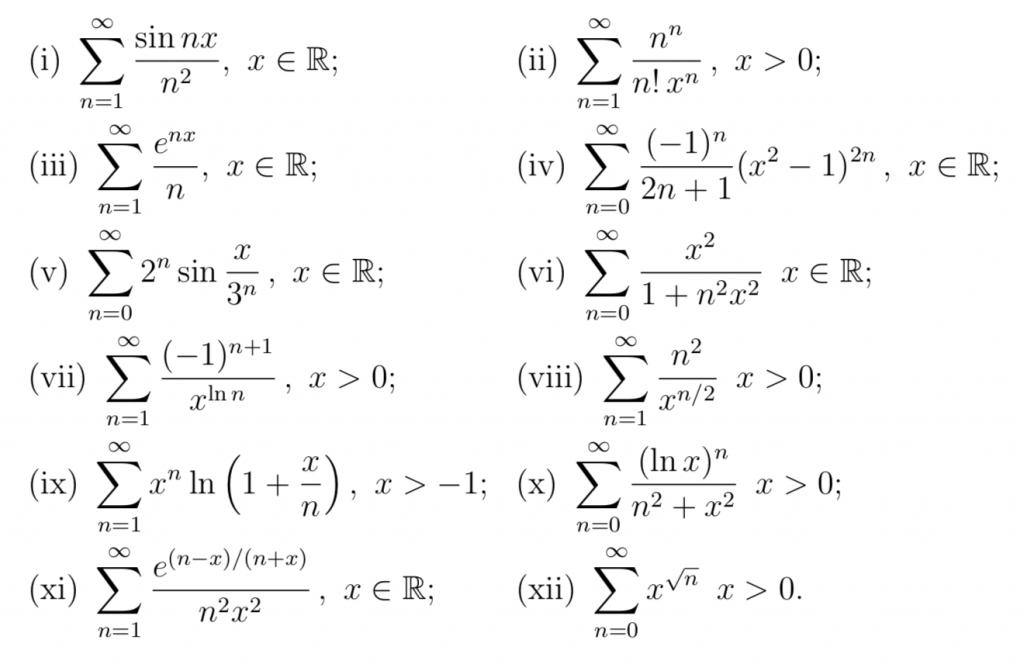
61. [Svolto il 28/3] Sia 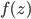 la somma della serie di potenze
la somma della serie di potenze 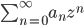 su
su 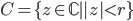 . Supponiamo che la serie converga in un punto
. Supponiamo che la serie converga in un punto 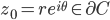 , con somma
, con somma 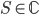 . Si provi che allora la serie converge uniformemente nel segmento di estremi
. Si provi che allora la serie converge uniformemente nel segmento di estremi 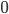 e
e 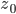 , e che
, e che 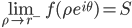 .
.
Una volta dimostrato questo, confronta con il più forte Teorema 6.33 delle note del corso!
62. Siano 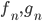 successioni di funzioni da uno spazio metrico in
successioni di funzioni da uno spazio metrico in  tali che
tali che
- la serie delle
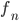 ha somme parziali uniformemente limitate in
ha somme parziali uniformemente limitate in  ;
; 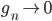 uniformemente su
uniformemente su  ;
;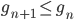 per ogni
per ogni 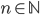 .
.
Si dimostri che la serie 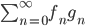 converge uniformemente su
converge uniformemente su  .
.
63. Sia 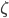 una radice primitiva
una radice primitiva 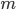 -esima dell'unità per
-esima dell'unità per 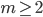 ; dimostrare che
; dimostrare che 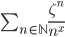 converge uniformemente sui compatti di
converge uniformemente sui compatti di 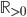 .
.
☞ 64. Si calcoli lo sviluppo in serie delle funzioni 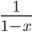 ,
, 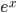 ,
, 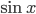 ,
,  ,
, 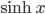 ,
, 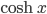 ,
, 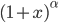 ,
, 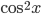 intorno a 0, se ne determini il raggio di convergenza e l'insieme di convergenza.
intorno a 0, se ne determini il raggio di convergenza e l'insieme di convergenza.
65. [Svolto il 28/3] Si dimostri che 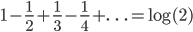 e che
e che 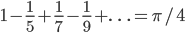 .
.
☞ 66. Data una matrice 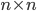 su
su 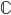 definiamo il suo esponenziale
definiamo il suo esponenziale 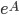 come
come \(\sum_{k=0}^{\infty} A^k/k\). Dimostrare che tale serie converge per ogni 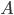 (nel senso della distanza indotta da una qualunque norma su
(nel senso della distanza indotta da una qualunque norma su 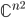 ). Mostrare inoltre che
). Mostrare inoltre che 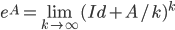 .
.
67. Si provi che, se 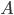 e
e 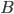 (matrici
(matrici 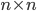 su
su 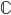 come sopra) commutano allora
come sopra) commutano allora 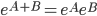 . È vero se
. È vero se 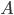 e
e 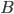 non commutano? Cosa si può dire sull'invertibilità della matrice
non commutano? Cosa si può dire sull'invertibilità della matrice 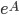 ?
?
68. Si dimostri che se 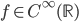 è tale che tutte le sue derivate siano non negative allora è analitica.
è tale che tutte le sue derivate siano non negative allora è analitica.
☞ 69. Si dimostri che 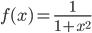 è analitica su tutto
è analitica su tutto  ma che il suo raggio di convergenza del suo sviluppo centrato in
ma che il suo raggio di convergenza del suo sviluppo centrato in 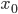 è
è 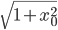 .
.
☞ 70. Calcolare il raggio di convergenza delle seguenti serie di potenze: