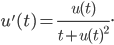Equazioni differenziali
83. Per ogni punto 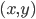 del piano con
del piano con 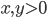 passa un’unica ellisse
passa un’unica ellisse 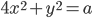 (con
(con 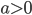 ). Descrivere la famiglia di curve che in ogni punto sono ortogonali all’ellisse passante per quel punto.
). Descrivere la famiglia di curve che in ogni punto sono ortogonali all’ellisse passante per quel punto.
84. Sia 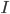 un intervallo aperto. Sia
un intervallo aperto. Sia 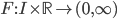 una funzione continua positiva, e sia
una funzione continua positiva, e sia 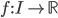 una funzione differenziabile che risolve l’equazione differenziale
una funzione differenziabile che risolve l’equazione differenziale 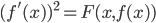 : mostrare che o
: mostrare che o 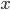 è sempre crescente, nel qual caso si ha
è sempre crescente, nel qual caso si ha 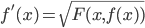 per ogni
per ogni 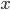 , oppure è sempre decrescente, nel qual caso si ha
, oppure è sempre decrescente, nel qual caso si ha 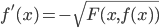 ; dunque
; dunque 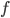 è di classe
è di classe 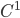 .
.
85. Descrivete tutte le funzioni 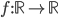 differenziabili che risolvono
differenziabili che risolvono 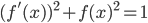 ; mostrare che sono
; mostrare che sono 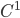 e in effetti
e in effetti 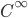 a tratti.
a tratti.
86. Sia ![f:[0,1]\to\mathbb{R}](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_2f88c23f13b9b1904c39f298cd688669.gif) una funzione
una funzione 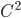 tale che
tale che 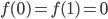 e
e 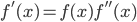 per ogni
per ogni ![x\in [0,1]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_c628ba2b1047de93f66cb815d986e107.gif) . Si provi che la funzione
. Si provi che la funzione 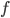 è identicamente nulla.
è identicamente nulla.
87. Determinare la soluzione generale dell’equazione differenziale
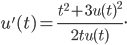
88. Discutere le soluzioni di
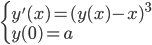
studiandone in modo qualitativo l’esistenza (locale o globale) delle soluzioni, le proprietà di monotonia e convessità/concavità.
89. Per il problema di Cauchy
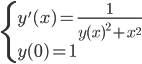
mostrate che esiste unica la soluzione globale 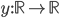 , e che
, e che 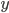 è limitata e esistono finiti i limiti
è limitata e esistono finiti i limiti 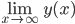 e
e 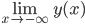 .
.
90.Discutete l’equazione differenziale
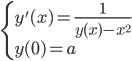
per 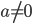 , studiando in modo qualitativo l’esistenza (locale o globale) delle soluzioni, le proprietà di monotonia e convessità/concavità. Mostrate che la soluzione esiste per tutti i tempi positivi, ma che per
, studiando in modo qualitativo l’esistenza (locale o globale) delle soluzioni, le proprietà di monotonia e convessità/concavità. Mostrate che la soluzione esiste per tutti i tempi positivi, ma che per 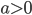 non si estende a tutti i tempi negativi. Mostrate che esiste un
non si estende a tutti i tempi negativi. Mostrate che esiste un 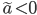 critico tale che, per
critico tale che, per 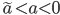 la soluzione non si estende a tutti i tempi negativi, mentre per
la soluzione non si estende a tutti i tempi negativi, mentre per 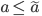 la soluzione esiste per tutti i tempi negativi; inoltre per
la soluzione esiste per tutti i tempi negativi; inoltre per  si ha
si ha 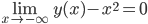 .
.
91. Consideriamo l’equazione differenziale 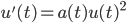 , dove
, dove 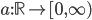 è una funzione continua. Dimostare che tutte le soluzioni con
è una funzione continua. Dimostare che tutte le soluzioni con 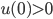 esplodono in tempo finito se e solo se
esplodono in tempo finito se e solo se 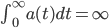 . L'ipotesi che
. L'ipotesi che 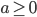 è davvero necessaria?
è davvero necessaria?
92. Si consideri il problema di Cauchy 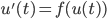 ,
, 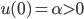 , dove
, dove 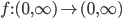 è una funzione continua. Dimostrare che c'è esistenza globale (nel futuro) se e solo se
è una funzione continua. Dimostrare che c'è esistenza globale (nel futuro) se e solo se 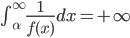 ,
,
93. Consideriamo l’equazione differenziale 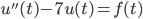 . Dimostrare che, se
. Dimostrare che, se 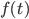 è una funzione continua e limitata, allora l’equazione ammette esattamente una soluzione limitata su tutta la retta.
è una funzione continua e limitata, allora l’equazione ammette esattamente una soluzione limitata su tutta la retta.
Consideriamo l’equazione differenziale 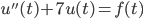 . Dimostrare che esiste una funzione
. Dimostrare che esiste una funzione 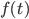 continua e limitata e tale che l’equazione non ammette nessuna soluzione limitata su tutta la retta.
continua e limitata e tale che l’equazione non ammette nessuna soluzione limitata su tutta la retta.
94. Consideriamo l’equazione differenziale
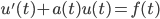 ,
,
dove 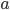 è un parametro reale ed
è un parametro reale ed 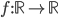 è una funzione continua.
è una funzione continua.
- Dimostrare che, se
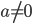 e
e 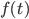 è limitata allora l’equazione ammette sempre esattamente una soluzione limitata su tutta la retta.
è limitata allora l’equazione ammette sempre esattamente una soluzione limitata su tutta la retta. - Dimostrare che, se
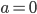 , allora le soluzioni sono tutte limitate o tutte illimitate, ed entrambi i casi si possono realizzare per opportune scelte di
, allora le soluzioni sono tutte limitate o tutte illimitate, ed entrambi i casi si possono realizzare per opportune scelte di 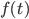 .
. - Dimostrare che, qualunque sia il valore di
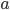 , se
, se 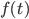 è periodica allora l’equazione ammette esattamente una soluzione periodica.
è periodica allora l’equazione ammette esattamente una soluzione periodica.
95. Determinare la soluzione generale dell’equazione differenziale