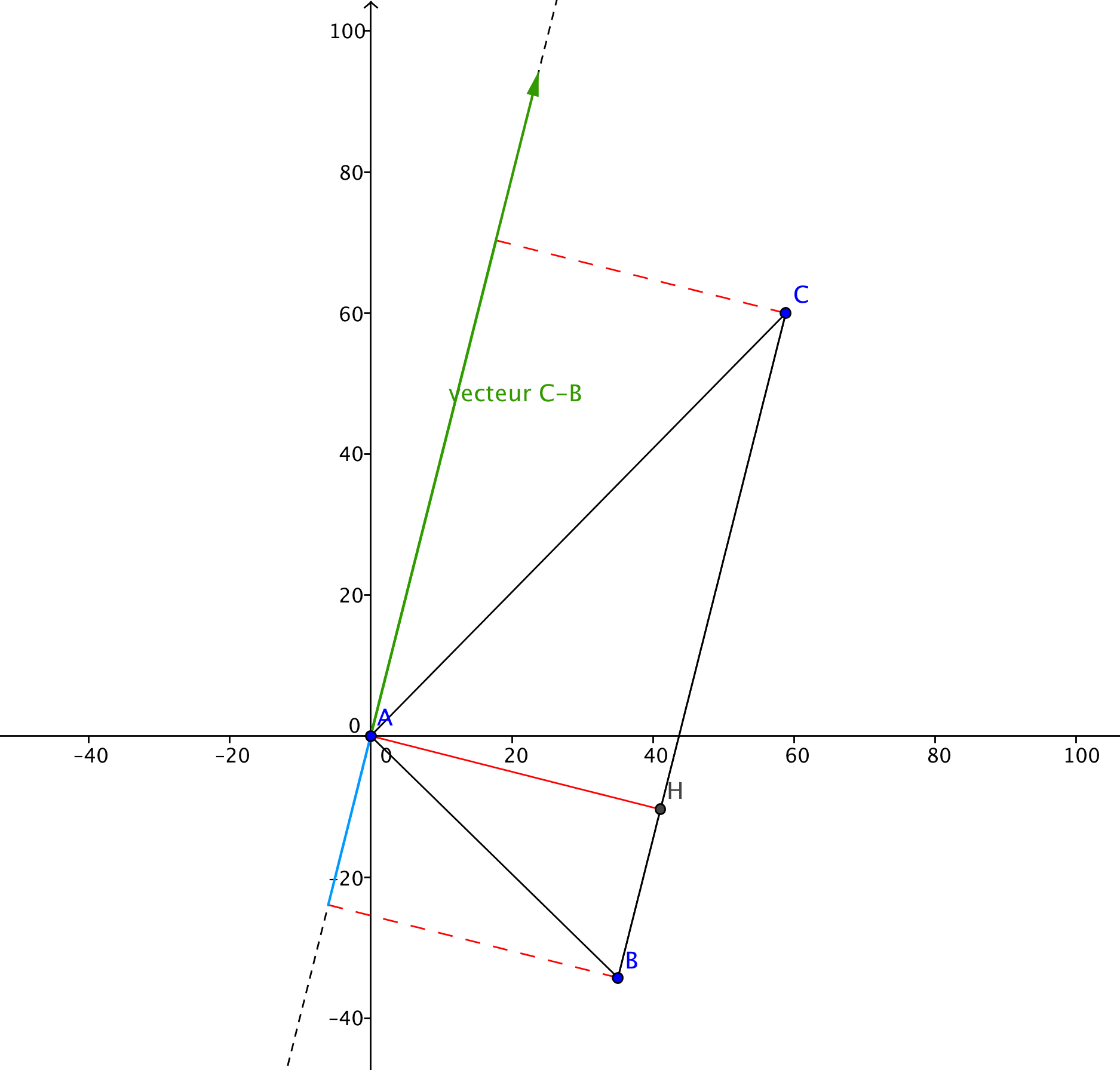
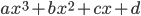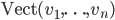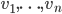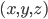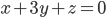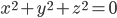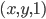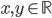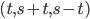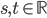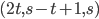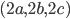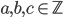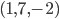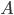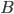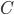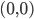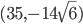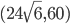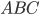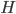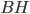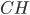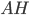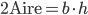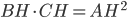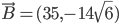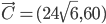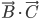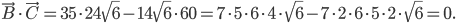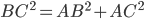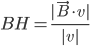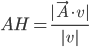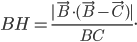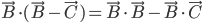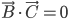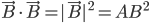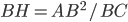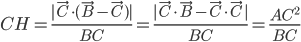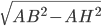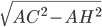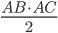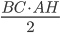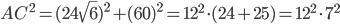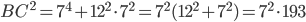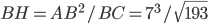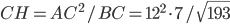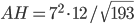Problème 2. On considère la droite de
d'équation
; soit
l'application linéaire qui à chaque vecteur du plan associe son symétrique par rapport à cette droite.
- Déterminer la matrice
associée à l'application
par rapport à la base canonique de
(au départ et à l'arrivée).
Soit 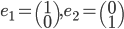 la base canonique de
la base canonique de  . Les colonnes de la matrice
. Les colonnes de la matrice 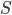 sont les vecteurs
sont les vecteurs 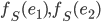 (exprimés dans la base canonique), donc on a simplement
(exprimés dans la base canonique), donc on a simplement
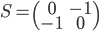 .
.
- Montrer que la matrice
(c'est-à-dire le produit entre la matrice
et elle même) est la matrice identité.
On a bien  .
.
- On considère la matrice
; quel est le noyau de l'application linéaire
correspondante ? Quelle est son image ?
On a
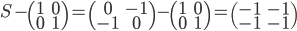
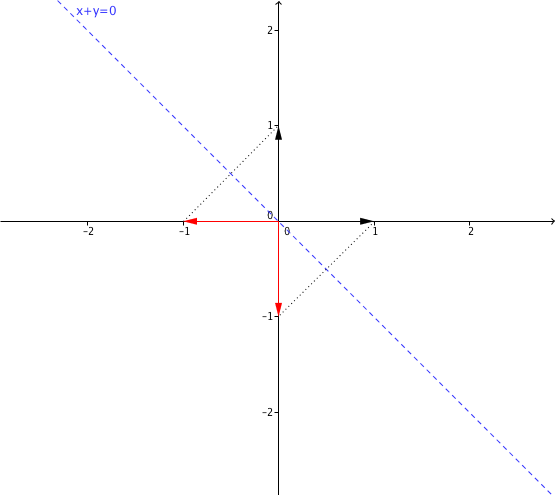
L'application linéaire 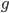 correspondante a comme image l'espace engendré par les colonnes de cette matrice, c'est-à-dire la droite engendrée par
correspondante a comme image l'espace engendré par les colonnes de cette matrice, c'est-à-dire la droite engendrée par 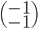 (autrement dit, la droite
(autrement dit, la droite 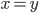 ).
).
Le noyau de 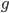 est l'ensemble des vecteurs
est l'ensemble des vecteurs 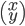 tels que
tels que 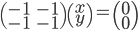 , c'est à dire tels que
, c'est à dire tels que 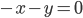 . Il s'agit donc de la droite
. Il s'agit donc de la droite 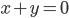 par rapport à laquelle on avait pris les symétriques.
par rapport à laquelle on avait pris les symétriques.
- Montrer que tout vecteur de
est orthogonale à tout vecteur de l'image de
.
Un vecteur de 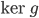 est de la forme
est de la forme 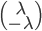 et un vecteur de l'image de
et un vecteur de l'image de 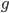 de la forme
de la forme 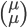 . Leur produit scalaire est
. Leur produit scalaire est  .
.
- Déterminer la matrice associée à
par rapport à la base
(au départ et à l'arrivée).
Les colonnes de la matrices sont les images des vecteurs donnés, exprimées en coordonnées par rapport à la base 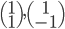 , que l'on va appeler
, que l'on va appeler 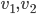 .
.
On a 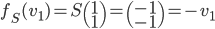 ; les coordonnées de
; les coordonnées de 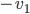 par rapport à la base
par rapport à la base 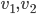 sont
sont 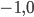 , donc la première colonne de la matrice sera
, donc la première colonne de la matrice sera 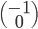 . On a
. On a 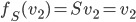 , qui a coordonnées
, qui a coordonnées 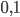 . La matrice cherchée est donc
. La matrice cherchée est donc 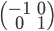 .
.
On sait que l'application linéaire
qui à chaque vecteur du plan associe son image par une rotation d'un angle
autour de l'origine est représentée par la matrice
(par rapport à la base canonique).
- Montrer que pour tout
et tout
le vecteur
a la même norme que le vecteur
.
Soit 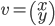 , alors
, alors 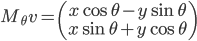 ; la norme de
; la norme de 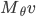 est la racine carrée de
est la racine carrée de 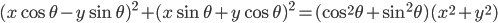 . Comme pour tout
. Comme pour tout 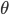
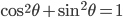 , la norme de
, la norme de 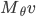 est
est 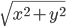 , c'est-à-dire la norme de
, c'est-à-dire la norme de 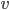 .
.
- Montrer que pour tout
on a
.
Remarquez que ça revient à dire que symétriser par rapport à la droite 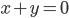 , faire une rotation de
, faire une rotation de 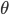 et puis symétriser encore une fois donne le même résultat que faire seulement une rotation de
et puis symétriser encore une fois donne le même résultat que faire seulement une rotation de 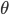 dans le sens inverse, ce qui se voit bien géométriquement.
dans le sens inverse, ce qui se voit bien géométriquement.
On peut aussi faire le calcul: on a

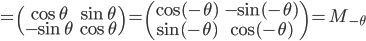 .
.
- Montrer que pour tout
on a
.
On a montré que 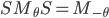 , donc
, donc 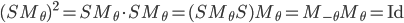 .
.
La dernière égalité est claire du point de vue des applications linéaire correspondantes, qui sont l'une l'inverse de l'autre, mais peut aussi être montrée en faisant les calcul du produit matriciel.




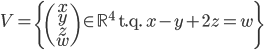
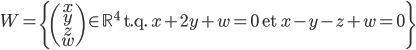
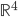
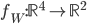
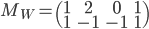
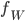
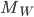
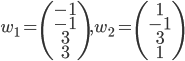
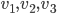
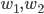
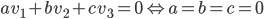
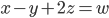
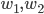
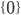

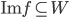
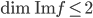
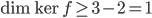
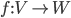
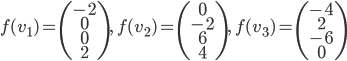
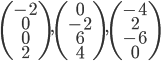
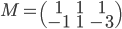
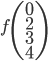
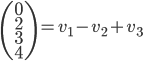

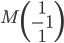
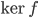
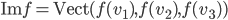
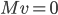
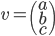
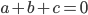
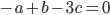
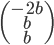
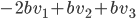
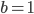
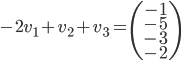
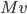
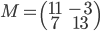
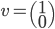
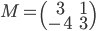
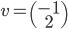
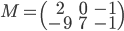
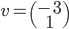
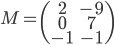
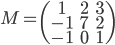
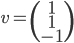
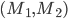
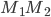
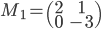
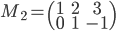
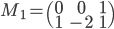
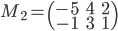
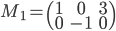
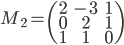
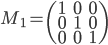
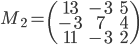
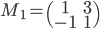
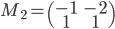
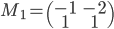
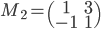
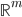
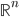
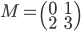
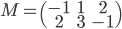
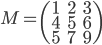
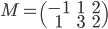
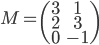
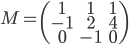
![f:\mathbb{R}[x]\to\mathbb{R}](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_851901561ae8a833b2329cd39ccd30d8.gif)
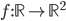
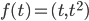
![f:\mathbb{R}[x]\to\mathbb{R}[x]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_145dc1ddf87117f11d547f8b90f72a21.gif)
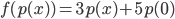
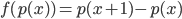
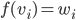
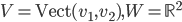
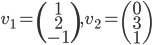
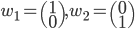
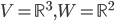

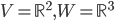

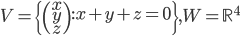
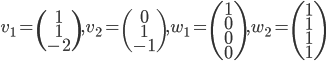
![f:\{ax^3+bx^2+cx+d\mbox{ t.q. }a,b,c,d\in\mathbb{R}\}\to\mathbb{R}[x] : f(p(x))=p'(x)](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_857f266940d4571f253f99e320ff7927.gif)


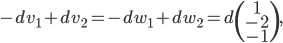

![\mathbb{R}[x]](http://alessandracaraceni.altervista.org/MyWordpress/wp-content/plugins/latex/cache/tex_52d4d6c0345834ef4ae2c597d02209d5.gif)